Марковские цепи. Дискретные марковские процессы, страница 2

Кроме вероятностей p(k) (k=1,2,…), часто интерес представляет асимптотическое поведение . Прежде чем перейти к этому вопросу введём классификацию состояний.

     5.2.Классификация состояний

Состояние i называется несущественным, если существует такое состояние j, в которое система может перейти за конечное число шагов из состояния i, но вернуться в состояние i вновь не может ни за какое число шагов, т.е. Все остальные состояния называют существенными. Далее мы будем говорить только  о таких состояниях.

Состояния i и j называются сообщающимися, если существуют такие числа m и k, что . Обозначают сообщающиеся состояния так: . Иначе говоря, состояние j достижимо из состояния i и наоборот. Свойство сообщаемости есть свойство эквивалентности. Действительно, 1) , согласно равенству (3); 2) из условия  следует ; 3) если  и , то . По определению существуют такие числа m и l, что . Согласно (2) имеем: .

Отсюда следует вывод: всё множество существенных состояний можно разделить на классы эквивалентности: в один класс эквивалентности попадают сообщающиеся состояния и ни из одного состояния данного класса нельзя перейти в какое-либо состояние другого класса. Такие классы называют по-разному: неприводимые, замкнутые, неразложимые.

Для иллюстрации рассмотрим МЦ с матрицей переходных вероятностей Р вида:

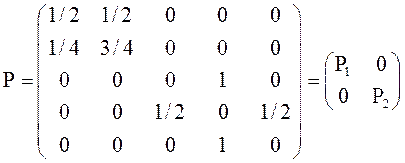. Состояние МЦ с такой матрицей Р распадается на два неприводимых класса сообщающихся состояний: {1, 2} и {3, 4, 5}. В зависимости от начальных условий процесс развёртывается либо в первом классе состояний и его переходы описывает подматрица Р₁, либо во втором и его переходы описывает подматрица Р₂.

Матрица Р – частный случай канонического вида матриц. Классификация состояний, приведённая выше, позволяет привести матрицу Р к каноническому виду. Для этого выделяют неприводимые классы и нумеруют их, отдельно выделяют несущественные состояния. Тогда матрица Р принимает вид:

Где P_l – матрица переходных вероятностей l-го неприводимого класса, B_s – матрица вероятностей перехода из несущественных состояний в s-й неприводимый класс, R – матрица вероятностей переходов по несущественным состояниям.

Заметим, что все понятия, связанные с сообщающимися состояниями, которые мы будем вводить далее, рассматриваются для матриц P в каноническом виде.

5.3.Периодичность состояний

Для некоторого состояния i обозначим множество m таких, что p_ii^m>0, символом M_i. Наибольший общий делитель (НОД) этих чисел из множества M_i обозначают через d_i и называют периодом состояния i. Если для всех  p_ii^m=0, то d_i=0 – это несущественное состояние.

Пример 3. В конечной марковской цепи с n состояниями и матрицей переходных вероятностей 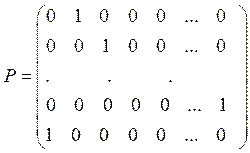  каждое состояние имеет период n.

Теорема 2. Если , то d_i = d_j.

Доказательство. Соотношение  означает, что существуют такие числа m и l, что p_ij^m>0и p_ji^l>0. Рассмотрим , т.е. m+l=0(mod d_i). Возьмем теперь вероятность возврата в состояние i за m+l+rd_i шагов, где r – любое число равное 0, 1, 2, …. Тогда  и rd_i= 0 (mod d). Так как r – любое число, то d_id_j. Аналогично можно показать, что d_jd_i  d_j = d_i.

Теорема 2 определяет период как характеристику класса сообщающихся состояний.