Марковские цепи. Дискретные марковские процессы, страница 3

Если d=1, то класс называется апериодическим или эргодическим.

Пусть d – период некоторого класса S состояний. Выберем из них одно i₀ и введём следующие подклассы класса S:

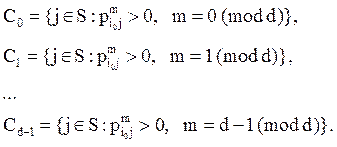
Покажем, что за один шаг система переходит в соседний класс, а из класса C_d-1 – в класс C₀. Пусть , p_ij>0. Покажем, что . Так как , то , но тогда за m+1 шаг система перейдёт в класс С_р+1: m+1=(p+1)(mod d), т.е.  и . По этой причине подклассы С_р называются циклическими подклассами ,.

Матрицу Р_l, неприводимого класса можно, таким образом, представить в виде:

	С0	С1	С2	…	Сd-1
С 0				…
С1				…
С2				…
…	…	…	…	…	…
Сd-1				…

В матрице штриховкой обозначены элементы, отличные от нуля. Если в начальный момент система находилась в подклассе С₀, то в момент времени k=p+dr, r=0,1,2, …, она будет находиться в подклассе С_p. Следовательно, с каждым подклассом C_p можно связать МЦ с вероятностями переходов  и этот класс будет неприводимым и апериодическим.

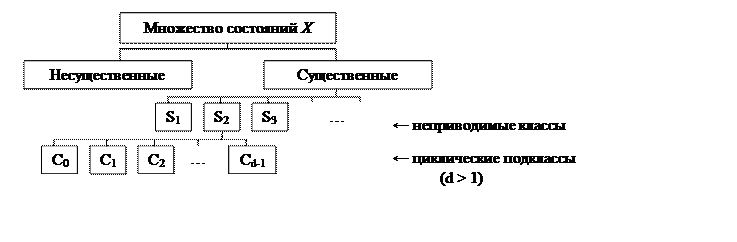
С учётом проведённой классификации все состояния МЦ можно представить в виде схемы:

        5.4. Возвратность

(5)

Для произвольного фиксированного состояния введём вероятность  того, что отправляясь из состояния i система впервые возвратится в это же состояние i через m переходов. Ясно, что , а . Значение  можно вычислить рекуррентно в соответствии с формулой:                                       

Формула (5) получается в результате следующих рассуждений. Рассмотрим всевозможные реализации процесса, для которых Х₀=i, Х_m=i, а первое возвращение в состояние i происходит на k-м шаге. Обозначим это событие E_k. События E_k, k=0, 1, …,m, являются несовместными, . Рассмотрим теперь те реализации, которые в течение оставшихся m-k шагов ведут себя так, что Х_m=i. Используя марковское свойство, имеем P(E_k)=P{первое возвращение происходит на k-м шаге| Х₀=i} P{Х_m=i|Х_k=i} = . Следовательно, . 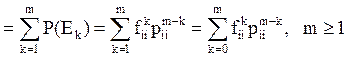Точно также можно ввести вероятность . Для вычисления  справедлива следующая рекуррентная формула:

(6)

Вероятность 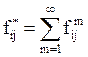можно рассматривать как вероятность того, что стартуя из состояния i система хотя бы один раз побывает в состоянии j.

Через  обозначим вероятность того, что система, выйдя из состояния i, не менее m раз побывает в состоянии j. В общем случае <1.

Если существует , то система, выйдя из состояния i, побывает в состоянии j бесконечное число раз.

Состояние i назовёмвозвратным, если , и невозвратным, если . Возвратность состояния i означает, что система, выйдя из состояния i, рано или поздно в него вернётся, но после возвращения в него эволюция системы как бы начинается заново.

Теорема 3.

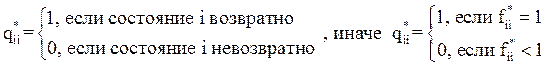
Доказательство. Обозначим через А событие вероятности , через E_k – событие вероятности , причём E₀ – событие, состоящее в том, что выйдя из состояния i система в него не вернётся. Тогда P(A|E_k)=Далее по формуле полной вероятности 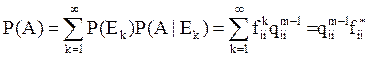. Полученную рекуррентную формулу  применим (m-1) раз: . В пределе при  получим, что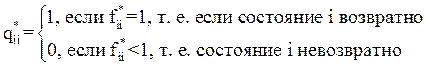

Теорема утверждает, что если состояние системы возвратно, то с вероятностью 1 система побывает в нем бесконечное число раз. Если же состояние невозвратно, то с вероятностью 1 система побывает в нем конечное число раз.

Теорема 4. Состояние i возвратно, если ряд  расходится.

 Доказательство. Пусть А – событие, состоящее в том, что система, выйдя из состояния i, вернётся в него за m шагов, быть может, и не впервые. События E_k, E₀ – как в теореме 3. Тогда P(A|E_k)=, P(A|E₀)=0 и  или