Исследование алгоритмов оптимального управления материальной точкой под действием силы при изопериметрическом ограничении

Исследование алгоритмов оптимального управления материальной точкой под действием силы при изопериметрическом ограничении

Рассмотрим различные методы решения задачи оптимального управления на примере динамики материальной точки под действием силы.

Динамика материальной точки под действием силы описывается следующей  системой уравнений

.

(1)

1.  Решение задачи оптимизации по критерию Больца

Критерий оптимальности системы (1.1) примем в виде функционала Больца

,	(2)
где ,  , .

Гамильтониан системы имеет вид

.

Для сопряженных переменных выполняются уравнения

 

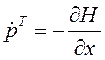
или в поэлементном виде  ()

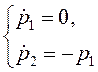
при граничных значениях, следующих из условий трансверсальности для задачи со свободным правым концом, , .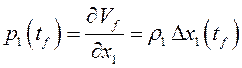

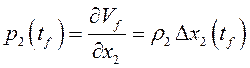Из условия 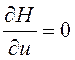 определим управление .

1.1. Найдем .  Тогда

=,,. Или ,  , .

Решение системы производилось при граничных условиях: ,

с, м, , м/с, . При выбранных граничных условиях с учетом выражений для  и , =1 и ,  управление имеет вид: . Результаты решения для этого случая представлены на рис.1.

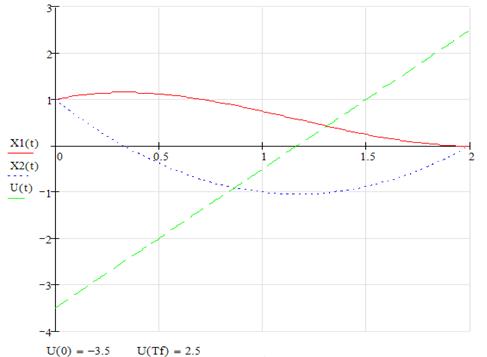Рис. 1. Графики зависимостей ,  и  

Можно также решить задачу численно методом Ньютона. Из условий трансверсальности следует . Поэтому зададим функцию невязки в виде 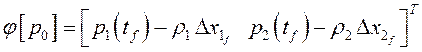 для случаев: а) , =0,  =…,  =…, б) , 0,  =…,  =0 (следовательно =0). В результате решения задачи управления получено: а) за … итерации: =…,  =…, б)  за … итерации: =…,  =… .

1.2. При   =0 полагаем =0 и 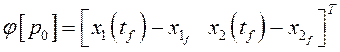. Выберем =10,  =20. В данном случае итерационная процедура выбора вектора  составляет 1 итерацию. В результате получено  =30,6,  =35,6 .        

2. Решение задачи оптимизации по критерию Красовского

Рассмотрим критерий качества управления в виде функционала Красовского:

.

(3)

Запишем гамильтониан задачи

.

Для сопряженных переменных выполняются уравнения

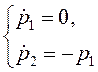
при граничных значениях , .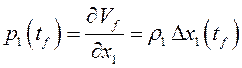

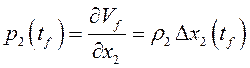На оптимальном решении , откуда находим . При этом

. Тогда канонические уравнения примут вид

	(4)
	(5)

Система уравнений  (4), (5) называется прогнозирующей моделью, так как в ней  и двухточечная краевая задача сводится к двум одноточечным задачам Коши: для системы (4)  в прямом времени при известных начальных (текущих) условиях с нахождением  и для системы (4), (5)  в обратном времени с граничными условиями для  и . В результате решения этих задач Коши определяются  и управление , с которым исходная система (1) интегрируется на 1 шаг вперед. Далее процедура в прогнозами в прямом и обратном времени повторяется из нового текущего положения точки. Из системы (5) находим  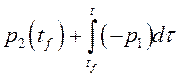= = = ,   . Тогда =, ==,=.

Управление имеет тот же вид, что и в п.1. Отличие состоит в вычислении граничных значений . В п.1 используется модель исходной системы с оптимальным управлением, а здесь при  получаем прогнозирующую модель. Однако в задаче со свободным начальным значением  численное решение методом Ньютона приводит к =0, следовательно, к =0, что совпадает с решением по критерию Красовского с заданным  по завершении переходного процесса .

2.1. На рис.1-рис.3 представлены результаты моделирования движения материальной точки при различных значениях , .

При  ,  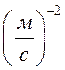- м, м/с

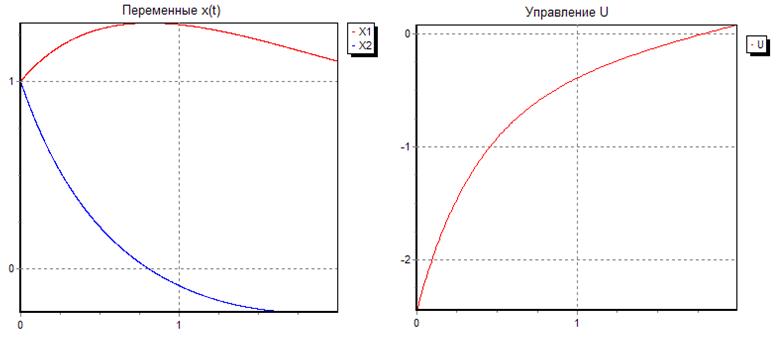
Рис. 2. Графики зависимостей ,  и

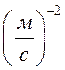При  ,  - м, м/с

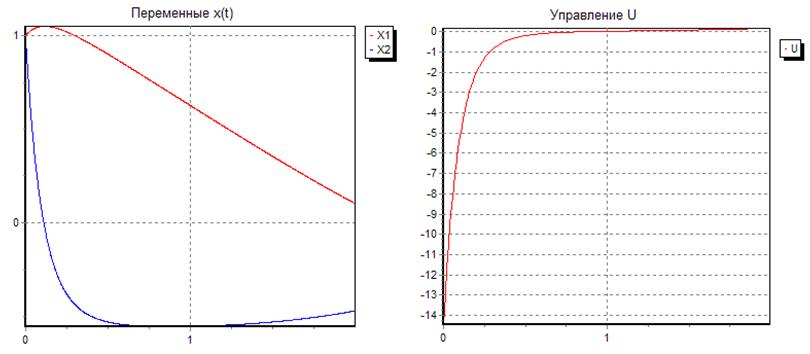
Рис. 3. Графики зависимостей ,  и

При  ,  - м, м/с.

При  ,  - м, м/с.

2.2. Если считать  не заданным и 0, то =0. Тогда можно вычислить  из условия  с применением уравнений прогнозирующей модели итерационным путем:  =,  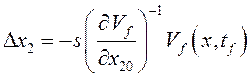и управление . Повторять итерации до выполнения условия  .

2.3. Видоизменим алгоритм с прогнозирующей моделью. При прогнозе уравнений системы на интервале  принимается  =0. Вычисляются граничные значения сопряженных переменных 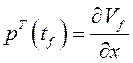.  Далее решается система уравнений модели и сопряженных переменных в обратном времени на интервале  и определяется зависимость , . С найденным управлением  интегрируется исходная система на интервале оптимизации .

3.  Решение задачи оптимизации по критерию Больца с изопериметрическим ограничением

В данном разделе рассмотрим задачу из пункта 1 при заданных начальных и конечных условиях (в формуле (3) полагаем =0) дополнительном интегральном  ограничении на площадь под кривой  на интервале оптимизации

.

(6)

Для решения этой изопериметрической задачи введем дополнительную переменную .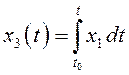

Гамильтониан системы имеет вид

.

Запишем канонические уравнения

(7)

(8)

при граничных значениях , , . Из системы (8) определяем

Из условия 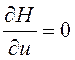 найдем управление  =.

Решим полученную двухточечную краевую задачу методом Ньютона.

Для этого введем вектор-функцию невязки

.

(9)