Исследование алгоритмов оптимального управления материальной точкой под действием силы при изопериметрическом ограничении, страница 5

Решение задачи для этого случая при начальных значениях = и =1 получено за … итерации. Окончательно получаем: , .

7.3. Если конечное положение считать заданным и рассмотреть критерий качества в виде 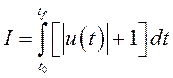, то в соответствии с условиями трансверсальности следует принять  функцию невязок в виде

.

Решение задачи для этого случая при начальных значениях = и =1, =… получено за … итерации. Окончательно получаем: , , =…

7.4. Если конечное положение считать свободным и рассмотреть критерий качества в виде ,  , , , то в соответствии с условиями трансверсальности следует принять  функцию невязок в виде

.

Решение задачи для этого случая при начальных значениях = и =1, =…  получено за … итерации. Окончательно получаем: , , =….

8.  Решение задачи максимального быстродействия с минимизацией затрат на управление и при ограничении на управление

Решим задачу управления системой (1) с использованием структуры управления, полученной в п.7 в виде:

, где . За дополнительное управление  принимается производная от моментов времени переключения управления   задачи из  п.7, т.е. , , .

В качестве минимизируемого выбирается критерий Больца

,  , , , .

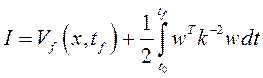Запишем гамильтониан задачи

..

Канонические уравнения примут вид

 

,

, а управление , . Здесь  и  - единичная и дельта-функции соответственно.

8.1. Решение задачи для этого случая при начальных значениях = и = =1 получено за … итерации. Окончательно получаем: , .

По завершении переходного процесса  получаем оптимальную программу , соответствующую решению задачи по принципу максимума.

8.2. При решении задачи для случая с незаданными начальными значениями   и  в вектор параметров функции невязок вместо  и   принимается:  и . Тогда решение задачи  при начальных значениях = и = =1 получено за … итерации. Окончательно получаем: , .

9.  Решение задачи максимального быстродействия с минимизацией затрат на управление и при ограничении на управление с фиксированной программой прогноза движения

Решим задачу управления системой (1) с использованием структуры управления, полученной в п.7 в виде:

, где . За дополнительное управление  принимается производная от моментов времени переключения управления   задачи из  п.7, т.е. , .

В качестве минимизируемого выбирается критерий Красовского

,  , , , .

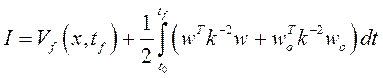Запишем гамильтониан задачи

..

Канонические уравнения прогнозирующей модели примут вид

 

,

, а управление , . Здесь  и  - единичная и дельта-функции соответственно.

Решение задачи для этого случая дает: , .

По завершении переходного процесса  получаем оптимальную программу , близкую к решению задачи из п.8 по принципу максимума.

10. Решение задачи методом Крылова-Черноусько

В этом случае вычисления проводятся в следующей последовательности.

1. Вводится начальная допустимая функция управления , i=1.

2. Решается исходная система при заданных начальных условиях на интервале  и вычисляется значение критерия .

3. В обратном времени на интервале совместно решаются исходная система уравнений  и система уравнений для сопряженных переменных при граничных условиях 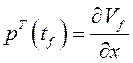.  Одновременно из условия инфимума гамильтониана в каждый момент времени вычисляется новое управление , .

4. Новое приближение для управления ищется в виде . Параметр s находится как и в методе Ньютона.

5. После нахождения  и вычисления величины  проверяется условие , где - число, определяющее точность решения краевой задачи. В случае невыполнения этого условия  итерации выбора управления продолжаются с п. 2. 

10.1. Решить задачу для критерия .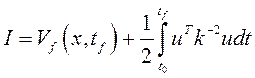

10.2. Решить задачу для критерия , .