Исследование алгоритмов оптимального управления материальной точкой под действием силы при изопериметрическом ограничении, страница 3

Из системы (11), (12) найдем 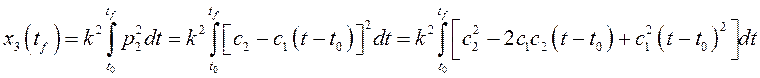и далее 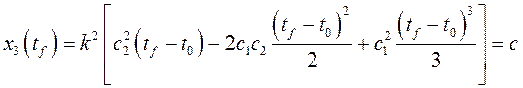. Задавая , из уравнения 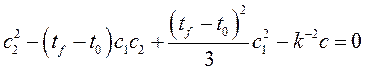 находим ==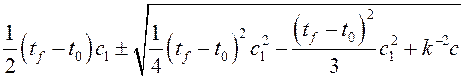  =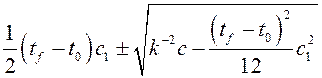. При =3, =2 имеем =3,53; =0,47.

Из условия  найдем управление  или , , .

Решим полученную двухточечную краевую задачу методом Ньютона.

Для этого введем вектор-функцию невязки

.

Зададим следующие значения параметров: =1, =0, =2 с, =0.1, =0.01, =1, =1м, =1м/с, =0, =0, =0, =C.

Результаты моделирования сведены в таблицу 2, где обозначено

.

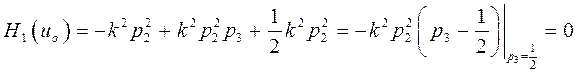Таблица 2 – результаты решения при изопериметрическом ограничении на управление

0	0,117	0,137	-12,277	-0,137	-0,258
0,1	0,390	0,455	-3,346	-0,455	-1,002
0,5	0,840	0,980	-1,286	- 0,980	-2,674
1,0	1,182	1,379	-0,769	-1,379	-4,314
2,0	1,668	1,945	-0,399	-1,945	-7,187
3,0	2,035	2,373	-0,237	- 2,373	-9,783
4,0	2,351	2,741	-0,138	- 2,741	-12,310
5,0	2,629	3,065	-0,071	- 3,065	-14,760
6,0	2,880	3,359	-0,021	- 3,359	-17,156
6, 5	2,998	3,496	0,000	- 3,496	-18,338
7,0	3,111	3, 628	0,018	-3, 628	-19,511
8,0	3,326	3, 879	0,049	-3, 879	-21,833
9,0	3,528	4,114	0,075	- 4,114	-24,127
10,0	3,719	4,337	0,097	- 4,337	-26,401
15,0	4,559	5,316	0,171	- 5,316	-37,563
20,0	5,261	6,135	0,215	-  6,135	-48,376
25,0	5,882	6,860	0,245	- 6,860	-59,058

На рис. 12 – рис. 17 представлены зависимости  от .

При наличии в критерии терминальной части   принимаем

.

Рис. 12. Графики зависимостей  от

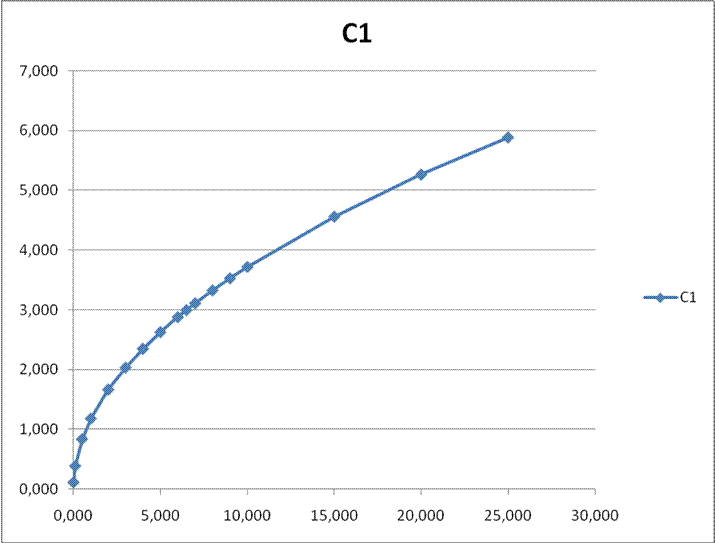
Рис. 13. График зависимости  от .

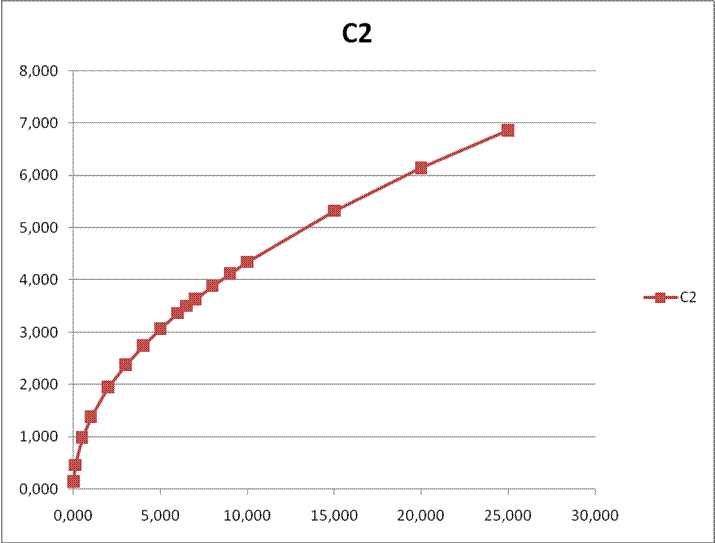
Рис. 14. Графики зависимостей  от  .

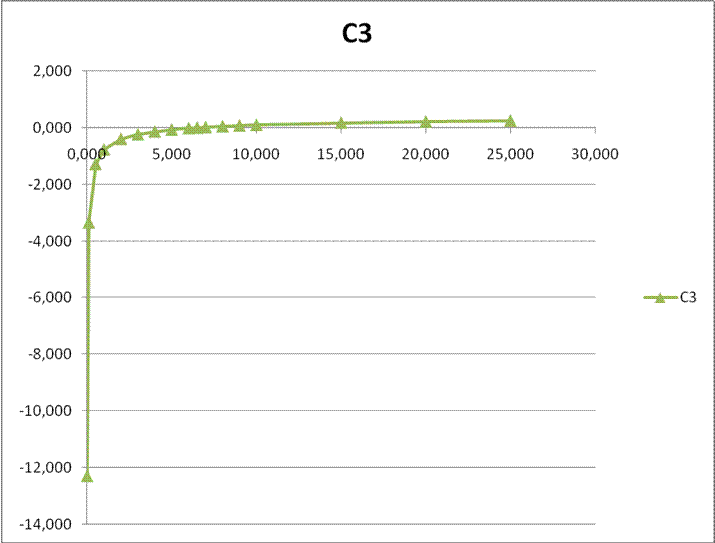
Рис. 15. График зависимости  от .

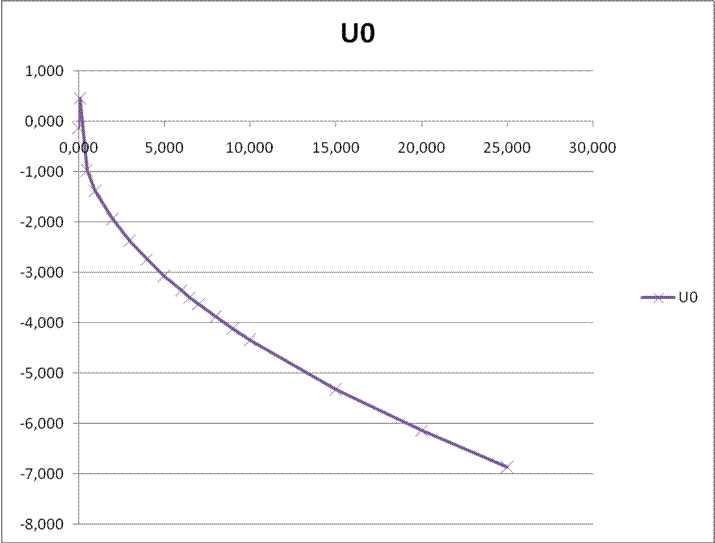
Рис. 16. График зависимости  от .

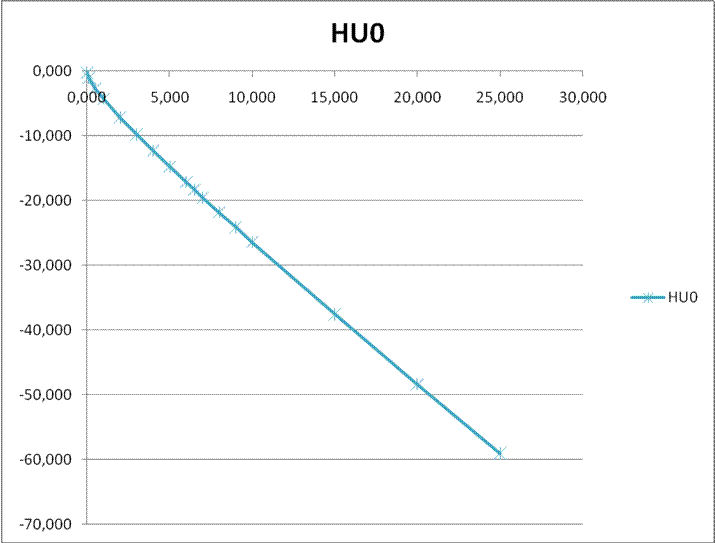
Рис. 17. График зависимости   от .

Поиск ограничения, не влияющего на управление

Рассмотрим систему (11) при  =0:

или

(13)

Система (13) аналогична системе (1). Опытным путем установлено, что  при С=6.5. Полученное решение представлено на рис. 18, рис. 19:

Рис. 1. Графики зависимостей ,  ,     .

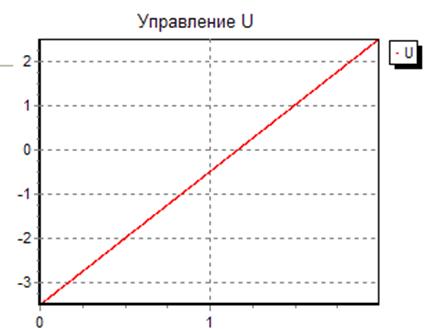
Рис. 19. График зависимости . 

Значение C=6.5 можно получить, вычислив  при управлении , найденном в пункте 1.

5.  Решение задачи максимального быстродействия при ограничении на управление

Рассмотрим задачу управления системой (1) для перевода ее из состояния  в состояние  при ограничении на управление  и при критерии качества 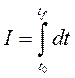, где  - заданная величина.

Гамильтониан исходной системы имеет вид

.