Исследование алгоритмов оптимального управления материальной точкой под действием силы при изопериметрическом ограничении, страница 4

Для сопряженных переменных выполняются уравнения , , откуда , где  - начальное условие для , .

Управление, минимизирующее гамильтониан, имеет вид

.

Граничные условия для и  ( и) удовлетворяют конечным условиям  .

Краевая задача может быть решена численно, например методом Ньютона. Для этого введем функцию невязок

и выберем некоторое начальное приближение для вектора , . Положим =1 н/кг=1 м/. Требуется перевести систему из заданного состояния =1м, =1 м/с в конечное =0 за минимальное время, =1.

При начальных значениях =метод Ньютона приводит к решению задачи за 4 итерации. Окончательно получаем: .

Если конечное положение считать свободным и рассмотреть критерий качества в виде ,  , , , то в соответствии с условиями трансверсальности следует принять  функцию невязок в виде

.

6.  Решение задачи оптимизации с фиксированной программой прогноза движения

Рассмотрим задачу управления системой (1) для перевода ее из состояния  в состояние  при ограничении на управление , где  - заданная величина.

Для упрощения процедуры вычисления управления можно применить алгоритм управления с фиксированной программой прогноза движения. При этом за дополнительное управление  принимается производная от момента  переключения управления , т.е. ,

.

В качестве минимизируемого выбирается критерий Красовского

,  , , .

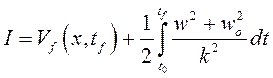Запишем гамильтониан системы 

,

, , , ;

(, , , ).

Уравнения прогнозирующей модели имеют вид:

 

, а управление . Здесь  и  - единичная и дельта-функции соответственно.

По завершении переходного процесса  получаем оптимальную программу , соответствующую решению задачи максимального быстродействия по принципу максимума.

Результаты моделирования при =2,1, =1, =1, =2с при шаге интегрирования =0,01с имеют вид: =1,24с, =0,008м, =-0,008м. Алгоритм устойчиво работает при достаточно больших отклонениях в задании начальных условий для   без изменения параметров , ,  критерия.

Если считать  не заданным и 0, то =0. Тогда можно вычислить  из условия  с применением уравнений прогнозирующей модели итерационным путем:  =,  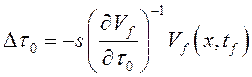и управление . Повторять итерации до выполнения условия  .

7.   Решение задачи максимального быстродействия с минимизацией затрат на управление и при ограничении на управление

7.1. Рассмотрим задачу управления системой (1) для перевода ее из состояния  в состояние  при ограничении на управление  и при критерии качества 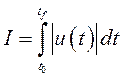, где  - заданная величина.

Гамильтониан исходной системы имеет вид

=

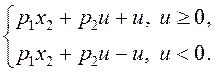
Для сопряженных переменных выполняются уравнения ,

, откуда , где  - начальное условие для , .

Из принципа максимума имеем . Отсюда находим  управление

Управление является релейной функцией с зоной нечувствительности.

Граничные условия для и  ( и) удовлетворяют конечным условиям  .

Краевая задача может быть решена численно, например методом Ньютона. Для этого введем функцию невязок

и выберем некоторое начальное приближение для вектора . Положим =1 н/кг=1 м/. Требуется перевести систему из заданного состояния =1м, =1 м/с в конечное =0 за время =3с, =1.

При начальных значениях =метод Ньютона приводит к решению задачи за … итерации. Окончательно получаем: , .

7.2. Если конечное положение считать свободным и рассмотреть критерий качества в виде 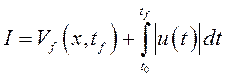,  , , , то в соответствии с условиями трансверсальности следует принять  функцию невязок в виде

.