Здесь![]() .
.
Зададим следующие значения параметров: ![]() =1,
=1, ![]() =0,
=0, ![]() =2 с,
=2 с, ![]() =0.1,
=0.1, ![]() =0.01,
=0.01, ![]() =1,
=1, ![]() =1м,
=1м, ![]() =1м/с,
=1м/с, ![]() =0,
=0, ![]() =0,
=0, ![]() =0,
=0, ![]() =с.
=с.
Результаты моделирования сведены в таблицу 1, где введено обозначение
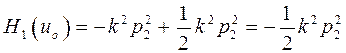 .
.
Таблица 1 – результаты решения при изопериметрическом ограничении
|
с |
|
|
|
|
|
|
0 |
32,941 |
13,465 |
14,982 |
-13,465 |
-90,649 |
|
0,1 |
30,697 |
12,718 |
13,860 |
-12,718 |
-80,870 |
|
0,5 |
21,718 |
9,727 |
9,369 |
-9,727 |
-47,309 |
|
1,0 |
10,499 |
5,990 |
3,758 |
-5,990 |
-17,939 |
|
1,2 |
6,016 |
4,497 |
1,515 |
-4,497 |
-10,112 |
|
1,333 |
3,035 |
3,504 |
0,024 |
-3,504 |
-6,141 |
|
1,4 |
1,533 |
3,004 |
-0,727 |
-3,004 |
-4,513 |
|
4,0 |
-56,718 |
-16,394 |
-29,867 |
16,394 |
-134,381 |
|
5,0 |
-79,180 |
-23,872 |
-41,105 |
23,8725 |
-284,945 |
|
6,0 |
-101,685 |
-31,365 |
-52,365 |
31,365 |
-491,885 |
|
7,0 |
-124,177 |
-38,854 |
-63,617 |
38,854 |
-754,820 |
|
8,0 |
-146,652 |
-46,338 |
-74,860 |
46,338 |
-1073,601 |
|
9,0 |
-169,156 |
-53,831 |
-86,119 |
53,831 |
-1448,912 |
|
10,0 |
-191,641 |
-61,319 |
-97,367 |
61,319 |
-1879,983 |
|
15,0 |
-304,100 |
-98,766 |
-153,626 |
98,766 |
-4877,405 |
|
20,0 |
-416,544 |
-136,210 |
-209,876 |
136,210 |
-9276,594 |
|
25,0 |
-529,004 |
-173,659 |
-266,135 |
173,659 |
-15078,712 |
На рис. 4 – рис. 9 представлены зависимости ![]() от
от ![]() .
.
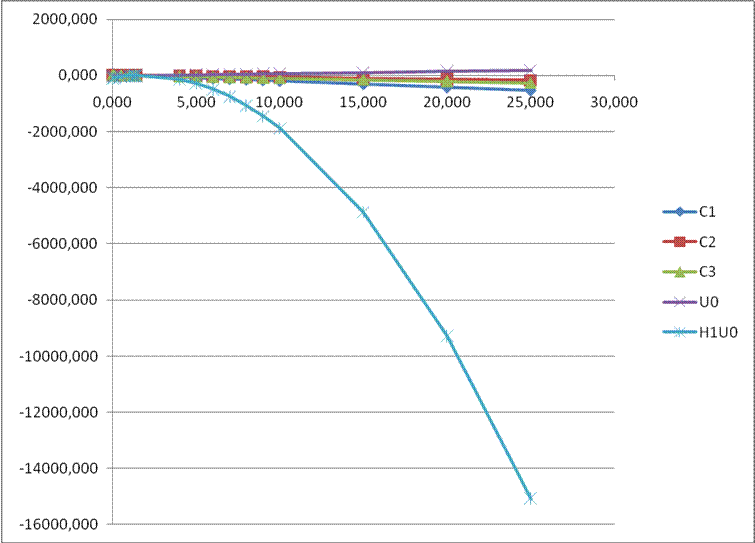
Рис. 4. Графики
зависимостей ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() от
от ![]()
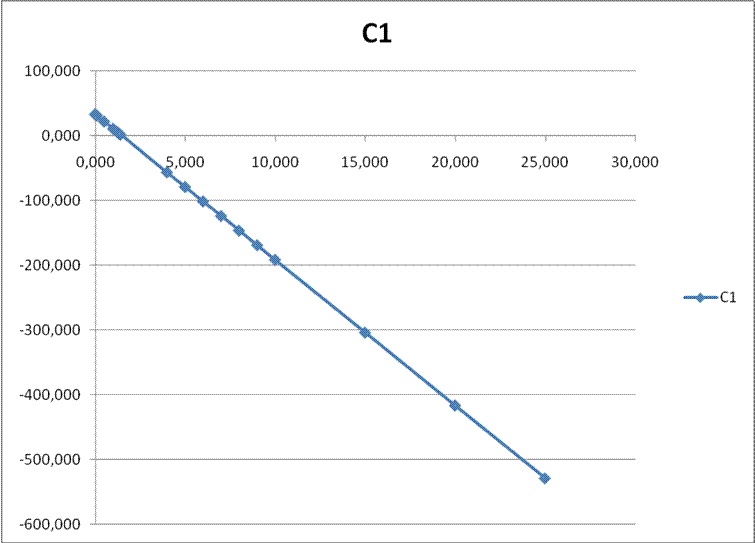
Рис. 5. График
зависимости ![]() от
от ![]()
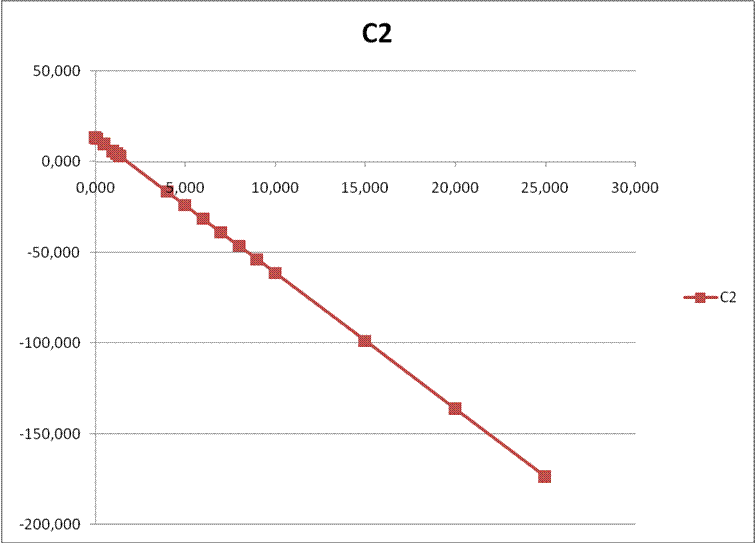
Рис. 6. График
зависимости ![]() от
от ![]()
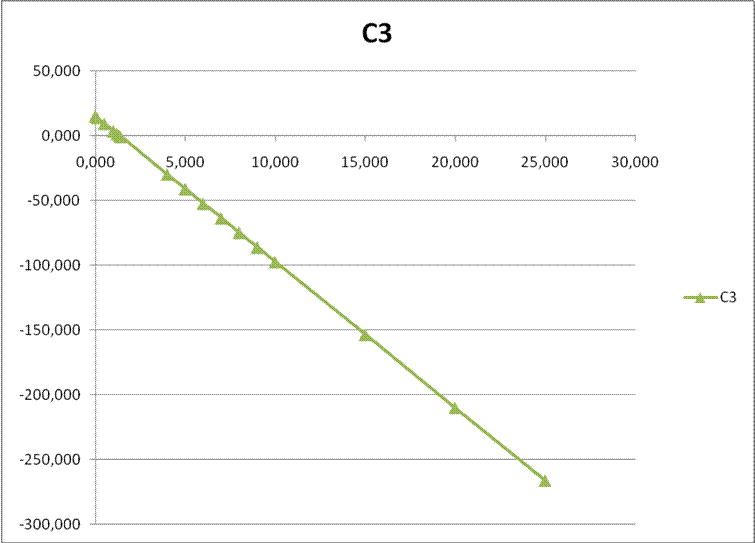
Рис. 7. График
зависимости ![]() от
от ![]()
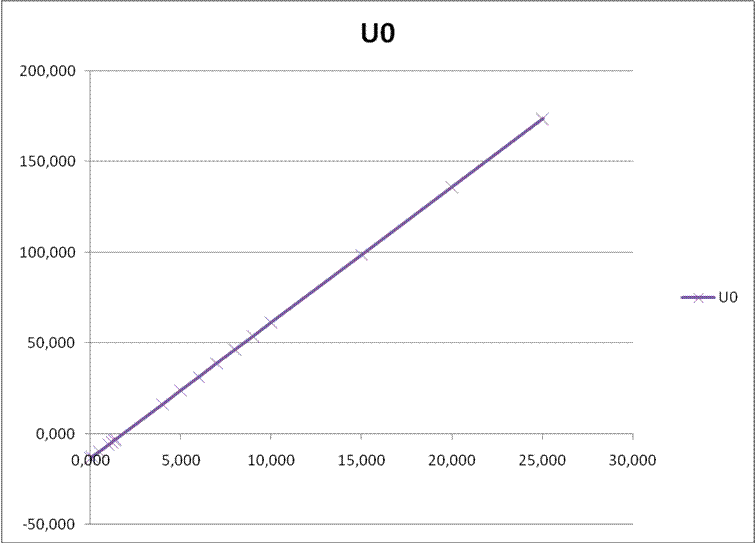
Рис. 8. График
зависимости ![]() от
от ![]()
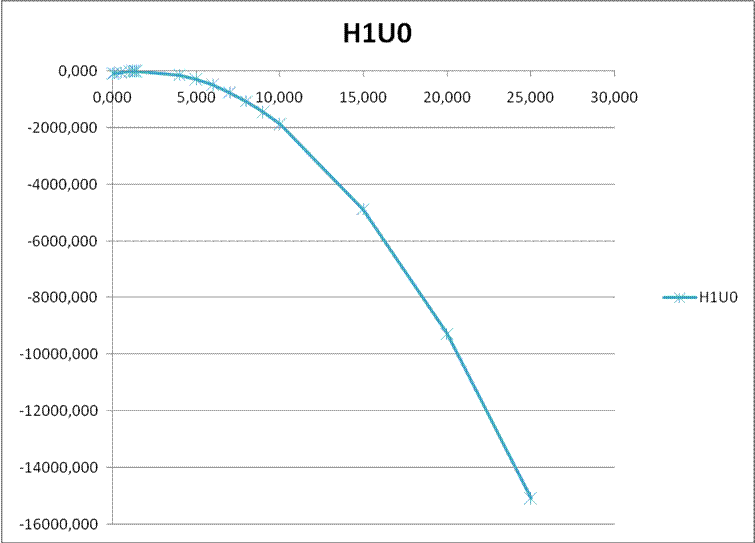
Рис. 9. График зависимости ![]() от
от![]()
Подберём ограничение ![]() таким образом, чтобы получить решение, аналогичное результатам
оптимизации по критерию Больца из п.1. Для этого с использованием
результатов моделирования
таким образом, чтобы получить решение, аналогичное результатам
оптимизации по критерию Больца из п.1. Для этого с использованием
результатов моделирования ![]() из п.1 вычислим
интеграл:
из п.1 вычислим
интеграл:
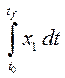 =1.33.
=1.33.
Тогда система (7) будет аналогична системе (1) при ![]() =1.33. Полученное решение можно увидеть на
рис. 10, рис. 11:
=1.33. Полученное решение можно увидеть на
рис. 10, рис. 11:
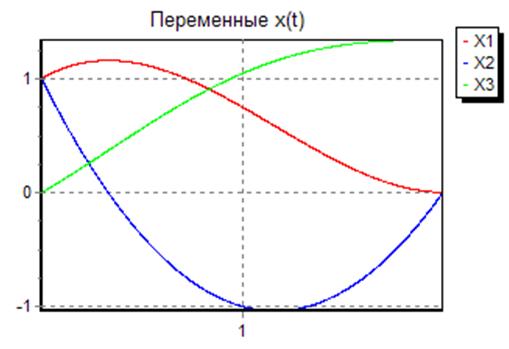
Рис. 10. Графики
зависимостей ![]() ,
, ![]() ,
, ![]()

Рис. 11. График зависимости ![]() .
.
В данном разделе рассмотрим задачу из пункта 1 при
заданных начальных и конечных условиях (в формуле (3) полагаем ![]() =0) дополнительном интегральном
ограничении на площадь под кривой
=0) дополнительном интегральном
ограничении на площадь под кривой ![]() на интервале
оптимизации
на интервале
оптимизации
|
|
(10) |
Для решения этой изопериметрической задачи введем
дополнительную переменную 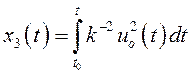 .
.
Гамильтониан системы имеет вид
![]() .
.
Запишем канонические уравнения
|
|
(11) |
|
|
(12) |
при
граничных значениях ![]() ,
, ![]() ,
, ![]() . Из системы (12) определяем
. Из системы (12) определяем
|
|
![]() ,
,![]() .
.
Причем ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.