Решение задачи максимального быстродействия с минимизацией затрат на управление и при ограничении на управление

БАЛТИЙСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ  "ВОЕНМЕХ" им.  Д. Ф.  УСТИНОВА

Кафедра И3

ОТЧЕТ ПО ДОМАШНЕМУ ЗАДАНИЮ

учебной дисциплины  «Методы оптимизации»

Решение задачи максимального быстродействия

с минимизацией затрат на управление

и при ограничении на управление

студентов:

            Назарова Р.С.                     

^{(Ф.И.О. студента)}

            Опенько С.В.          

^{(Ф.И.О. студента)}

            Попова А.И.            

^{(Ф.И.О. студента)}

группы  И393

ПРЕПОДАВАТЕЛЬ:                                

Кабанов С.А.           //

^{(Ф.И.О. преподавателя)              (подпись преподавателя)}          

“”2012  г.

САНКТ-ПЕТЕРБУРГ

2012 г.

Оглавление

Введение. 3

Постановка задачи. 4

Решение. 5

Блок-схема программы.. 7

Исходный код программы на языке MathCad. 8

Результат работы программы.. 10

Заключение. 12

Список использованной литературы.. 13

Введение

Объекты, с которыми имеет дело техника, обычно снабжены «рулями» — с их помощью человек управляет движением. Математически поведение такого объекта описывается некоторыми уравнениями, куда входят и управляющие параметры, характеризующие положение «рулей». Естественно, возникает вопрос об отыскании наилучшего (оптимального) в том или ином смысле управления движением. Например, речь может идти о достижении цели движения за минимальное время. Этот вопрос является задачей вариационного исчисления. В отличие от классических вариационных задач, где управляющие параметры меняются в некоторой открытой области (без границы), теория оптимальное управление охватывает и тот случай, когда управляющие параметры могут принимать и граничные значения. Последнее обстоятельство особенно существенно с прикладной точки зрения, поскольку при управлении техническим объектом именно положение «руля» «на упоре» часто обеспечивает оптимальное управление.

Центральным результатом теории оптимальное управление, является принцип максимума Понтрягина, дающий общее необходимое условие оптимальности управления. Этот результат и связанные с ним исследования, проведённые Л. С. Понтрягиным и его сотрудниками, послужили исходным пунктом разработки теоретических, вычислительных и прикладных аспектов теории оптимальное управление.

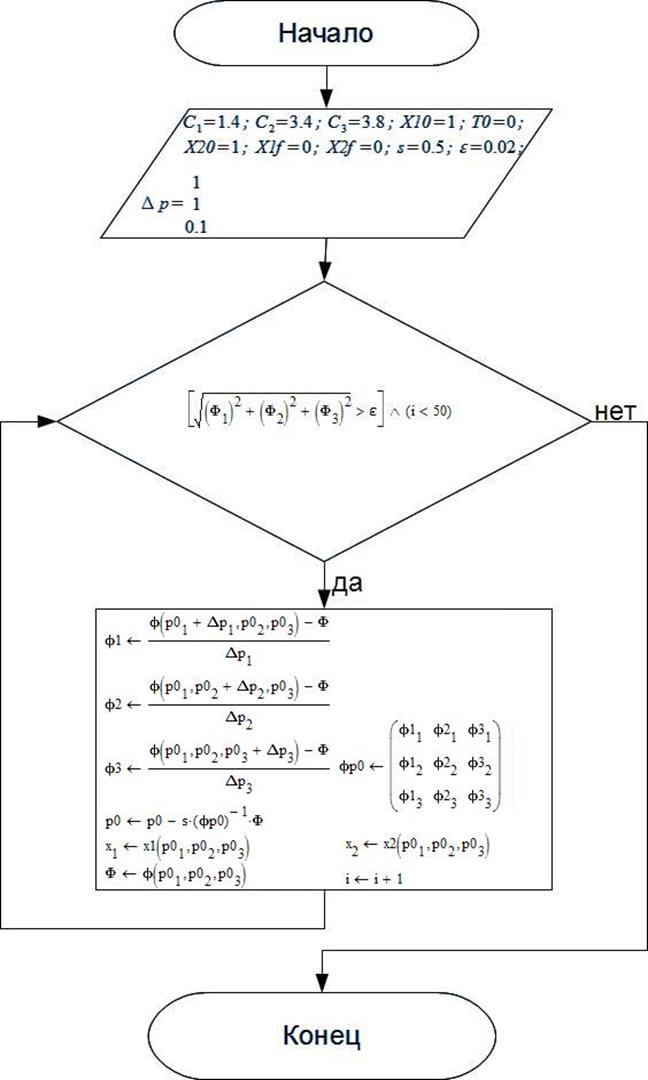
В данной работе рассматривается численное решение и отладка задачи максимального быстродействия при ограничении на управление по методу Ньютона. В ходе работы будут определены наилучшие начальные значения и установятся зависимости после их изменения.

Постановка задачи

Необходимо при помощи управления перевести систему (1) из состояния x(t₀) в состояние x_f  при ограничении на управление  и при критерии качества 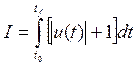, где u_m- заданная величина.

,           (1)

,

,

.

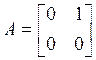Положим:

u_m=1 н/кг=1 м/с²,

x₁(t₀)=1 м,

x₂(t₀)=1 м/с,

x_1f =x_2f =0,

t₀=0 c,

∆p₁ = ∆p₂=1, ∆p₃=0.1 .

Решение

Гамильтониан исходной системы имеет вид:

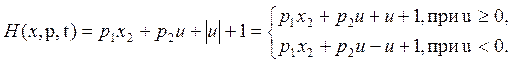
Для сопряженных переменных выполняются уравнения:

,

, откуда p₁=c₁, p₂(t)= c₂- c₁(c₃-t₀), где c_i - начальное условие для p_i , i=1,2,3.

Из принципа максимума имеем:

Отсюда находим управление:

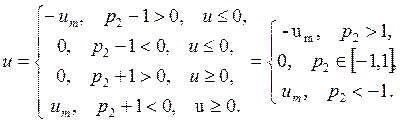
Управление является релейной функцией с зоной нечувствительности. Граничные условия для p₁ и p₂ (c₁ и c₂)  удовлетворяют конечным условиям  x(t_f)=x_f .

Данная краевая задача может быть решена численно, методом Ньютона. В соответствии с условиями трансверсальности следует принять функцию невязок в виде:

.

Выбирается некоторое начальное приближение для вектора .

Из условия 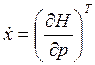получаем:

,

.

В результате, - система будет иметь вид:

 

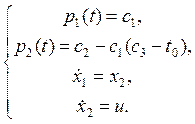
Решение задачи методом Ньютона включает в себя следующие шаги:

1.  Выбирается некоторое начальное приближение .

2.  Решается - система с начальными условиями , на интервале .

3.  Вычисляется вектор .

4.  В соответствии с формулой Тейлора, , откуда

5.  Определяется следующее приближение для вектора p₀: , где скалярный множитель . Выбор величины s происходит из требования . В качестве нормы  принимают либо , либо .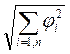

6.  Проверяется условие , i = 1, 2, …, невыполнение которого возвращает алгоритм к п.1.  Здесь - любая малая положительная величина.

Матрица  – обратная матрице частных производных .

Блок-схема программы

 

Исходный код программы на языке MathCad

Результат работы программы

При начальных значениях  и , , за 39 итераций окончательные значения получаются следующими: , .

График для данного случая:

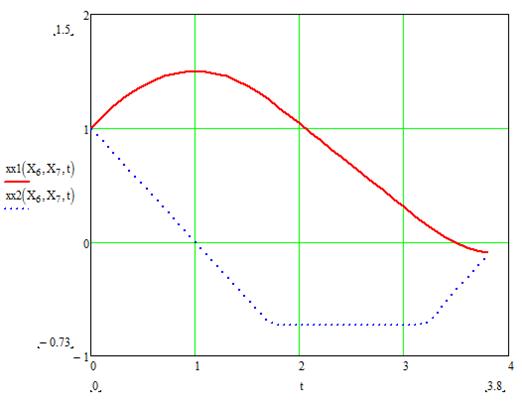
Также необходимо отметить, что шаг интегрирования был взят равным 0.1.

При изменении ,  за 11 итераций окончательные значения получаются следующими: , .

График для данного случая:

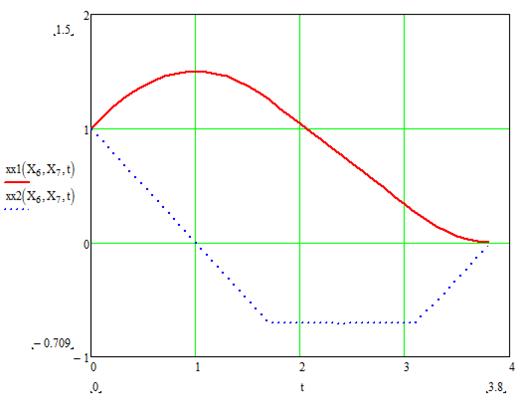
При изменении  за 4 итерации окончательные значения получаются следующими: , .

График для данного случая:

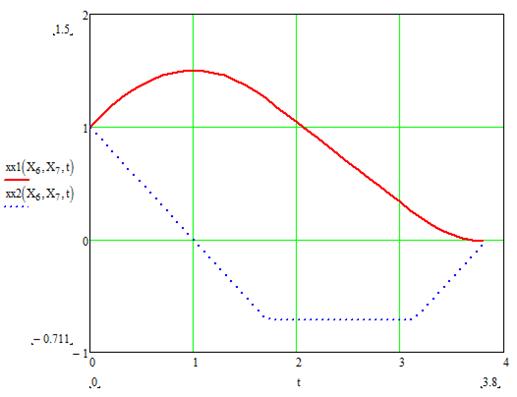
При изменении  и  за 2 итерации окончательные значения получаются следующими: , .

График для данного случая:

Заключение

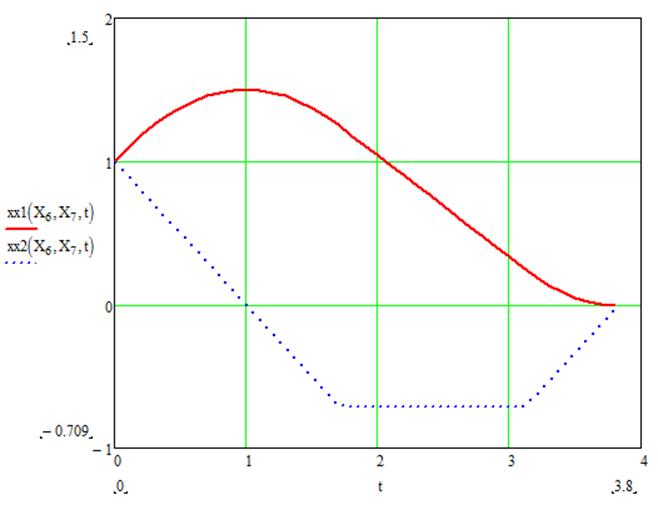
Собрав необходимую информацию и алгоритмически описав решение, в соответствии с заданием было разработано приложение, реализующее численное решение двухточечной краевой задачи методом Ньютона. В качестве среды программирования был выбран MathCad, т.к. он отвечает всем необходимым требованиям для разработки