Первые уроки по изучению площади

С.Е. ЦАРЕВА. Первые уроки по изучению площади // Начальная школа, 1981. - №10. – с.39-42.

Основная задача изучения геометрического материала в III классе — формирование у уча­щихся общих представлений о площади и вы­работка умения вычислять площадь прямо­угольника. Наблюдения за выполнением зада­ний по определению площади прямоугольника показывают, что овладение учащимися этим умением часто оказывается формальным.

С целью устранения указанного недостатка в математической подготовке третьеклассников в 1979 году в программу и в учебник были внесены некоторые изменения, а именно: иск­лючена формула площади прямоугольника S = а* b. Однако отказ от применения фор­мул еще не решает проблему полностью.

Для формирования осознанного умения опре­делять площадь прямоугольника очень важны первые уроки по изучению площади. Не­достаточное внимание учителей на этих уро­ках к упражнениям, направленным на обес­печение понимания детьми конкретного смыс­ла измерения площади, является, на наш взгляд, одной из причин отмеченного недостат­ка в знаниях учащихся.

На вопрос “Что значит измерить площадь прямоугольника?” дети чаще всего отвечают так: “Это значит, что нужно измерить длину и ширину прямоугольника и найти произведе­ние полученных чисел”. Но ведь найти пло­щадь прямоугольника (в квадратных сантимет­рах) — это значит определить, сколько квад­ратных сантиметров содержится в нем. Уча­щиеся смешивают понятие измерение площади со способом   рационального ее вычисления.

При таком смешении у учащихся создается представление о качественном различии поня­тий площадь фигуры (отличной от прямо­угольника), ограниченной ломаной, площадь прямоугольника, площадь криволинейной фи­гуры, так как для измерения площади каж­дой из этих фигур применяются различные спо­собы. Это мешает учащимся при вычислении площади прямоугольника осуществлять само­контроль за своей деятельностью путем при­влечения общих представлений о площади и ее измерении.

Для предотвращения неправомерного разде­ления качественно однородных понятий и при­вития таких способов рассуждений, которые помогли бы им осуществлять самоконтроль при вычислении площадей прямоугольников, следует тщательно отрабатывать упражне­ния, предшествующие вычислению площади прямоугольника по правилу и направленные на формирование представлений о конкретном смысле измерения площади. В своей статье мы и хотим показать, как это лучше сделать.

Ознакомление учащихся с термином площадь и первичное знакомство со сравнением площадей лучше провести в процессе выпол­нения упражнения, аналогичного упражнению 371 из учебника для III класса. Учитель по­казывает две фигуры, одна из которых поме­щена внутри другой, и спрашивает, как мож­но охарактеризовать взаимное расположение фигур. (Первая фигура находится внутри вто­рой.) Можно еще сказать, что первая фигура полностью помещается во второй. В этом слу­чае говорят, что площадь первой фигуры мень­ше площади второй фигуры, а площадь вто­рой фигуры больше площади первой фигуры.

Проверяя, как учащиеся усвоили новый тер­мин, учитель показывает еще пару моделей фигур, изготовленных из картона.

Как узнать, площадь какой фигуры больше? (Нужно наложить одну фигуру на другую) Учитель просит одного из учеников продемон­стрировать это. Ставятся вопросы: “Площадь какой фигуры больше?”, “Площадь какой фи­гуры меньше?”

После выполнения этого задания целесооб­разно провести практическую работу с разда­точным материалом. Каждому ученику дает­ся по две фигуры (они пронумерованы цифра­ми 1 и 2), которые могут быть у всех уча­щихся различными Важно лишь, чтобы одна из них полностью помещалась в другой. Для быстроты проверки результатов сравнения можно пронумеровать фигуры так, чтобы в каждой паре цифрой 1 была обозначена фи­гура с большей площадью. Учащимся дается задание: сравнить площади данных им фигур и выписать (или назвать) их номера в поряд­ке возрастания площади. Для записи ответов удобно использовать индивидуальные доски, так как в этом случае учитель видит ответы сразу всех учащихся. Во время выполнения работы он наблюдает, как дети проводят срав­нение.

Затем учитель опять переходит к фронталь­ной работе с классом. Он предлагает срав­нить на глаз, а затем путем наложения пло­щади двух таких фигур, по отношению к ко­торым вопрос не может быть решен тем же способом (см., например, фигуры, изображен­ные на рисунке 1. С обратной стороны эти фигуры разбиты на одинаковые  квадраты). Возникает проблемная ситуация. Учащиеся го­ворят, что путем наложения нельзя опреде­лить, площадь какой фигуры больше. Тогда учитель поворачивает фигуры обратной сто­роной. Учащиеся при этом обычно сами дога­дываются, как можно сравнить данные фигуры по площади. Кто-то из них пересчитывает число квадратов в каждой фигуре. Формули­руется вывод: если фигуры нельзя сравнить по площади наложением, то можно каждую из фигур разбить на одинаковые между собой фигуры (квадраты, треугольники) и затем под­считать, сколько их содержится в каждой фи­гуре. Фигура, в которой содержится большее число таких одинаковых фигур, имеет боль­шую площадь.

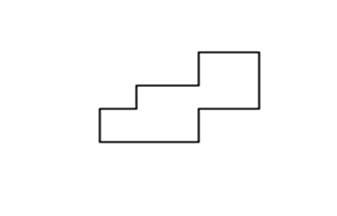
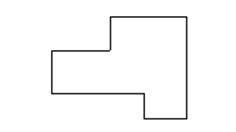
Рис.1.

Для закрепления проводится работа по таб­лице “Площади фигур” под руководством учи­теля, а затем учащиеся самостоятельно выпол­няют упражнения 374 и 375. Чтобы подчерк­нуть, что для сравнения площадей фигуры должны быть разбиты на одинаковые между собой части, предлагается следующее задание.

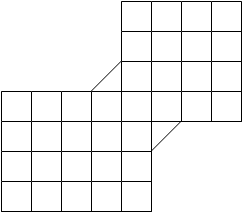
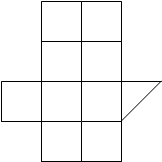
Учитель показывает две фигуры, разбитые так, как показано на рисунке 2.

 

Рис.2.

С помощью учителя дети приходят к выводу, что при таком разбиении сравнить площади фигур путем подсчета числа квадратов и тре­угольников, содержащихся в них, нельзя. (Ни в коем случае не должен прозвучать вывод, что эти фигуры вообще нельзя сравнить по площади.) Обратную сторону фигур можно разбить на одинаковые между собой фигуры и после вывода, сделанного выше, провести сравнение.

Для проверки усвоения нового материала и для его закрепления проводится практиче­ская работа. Учащимся раздаются листы клет­чатой бумаги, на которых изображены пять фигур, причем две из них — прямоугольники. Все фигуры пронумерованы (рис. 3).

Дается задание — сравнить площади данных фигур. Учащиеся подсчитывают число квадра­тов (клеточек), содержащихся в каждой фигу­ре, и результат записывают под соответст­вующей фигурой Можно предложить выпи­сать номера фигур в порядке возрастания площади.

 

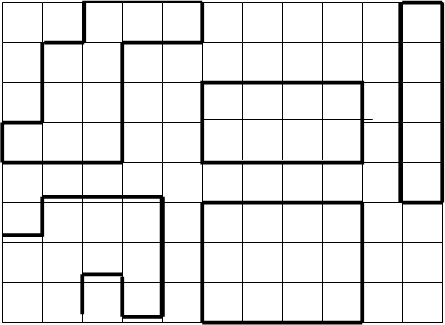Рис.3.

На втором уроке учащиеся знакомятся с единицей площади — квадратным сантимет­ром, учатся измерять площади фигур путем разбиения их на квадратные сантиметры с по­мощью линейки и карандаша, с помощью па­летки или путем покрытия фигуры моделями квадратных сантиметров. Опыт показывает большую эффективность использования на вто­ром уроке палетки и моделей квадратных сантиметров.

Не останавливаясь на содержании вводной беседы, во время которой учитель знакомит с понятием и термином квадратный санти­метр, покажем содержание и методику рабо­ты, направленную на осознание детьми смыс­ла измерения площади и формирование уме­ния измерять площадь фигур в квадратных сантиметрах.

К уроку готовится раздаточный материал; модели квадратных сантиметров, палетки, лис­ты нелинованной бумаги с изображениями геометрических фигур для проведения практи­ческой работы по измерению площади.

После введения квадратного сантиметра уча­щимся предлагается начертить в тетради квад­ратный сантиметр и написать 1 кв. см Затем они находят квадратный сантиметр у себя на партах, после чего проводят практическую ра­боту по заранее розданным листам, о которых говорилось выше.

Содержание листов у всех одинаково и может быть, например, таким (рис. 4)