Первые уроки по изучению площади, страница 2

Учитель последовательно организует работу с каждой фигурой.

Найдите на листе фигуру под номером 1. Покройте ее квадратными сантиметрами.

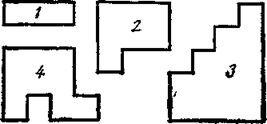
Рис.4.

Сколько квадратных сантиметров в фигуре 1? (3.) В этом случае говорят, что площадь фи­гуры 1 равна трем квадратным сантиметрам. Объясните, что значит, что площадь фигуры 1 равна трем квадратным сантиметрам. (Это зна­чит, что в фигуре 1 содержится 3 квадратных сантиметра.) Что такое квадратный санти­метр? (Это квадрат со стороной 1 см.) На листе под фигурой 1 учащиеся делают соответ­ствующую запись: 3 кв. см.

С помощью моделей квадратных сантимет­ров учащиеся измеряют также площадь фигу­ры 2 и результат записывают под ней. После выполнения этой работы учитель говорит, что ,так измерять площадь долго и трудно. Легче разбить фигуру на квадратные сантиметры с помощью линейки и карандаша и затем под­считать их число. Для определения площади фигуры 3 учащиеся расчерчивают ее на квад­ратные сантиметры и, подсчитав их, записывают результат под фигурой—14 кв. см.

Проверяя правильность выполнения задания, учитель не только просит назвать величину площади, но и спрашивает, что значит, что площадь фигуры равна, например, 14 кв см. (Это значит, что в фигуре содержится 14 квад­ратных сантиметров, т. е. 14 квадратов со сто­роной 1 см.)

Следующий этап — знакомство с палеткой и измерение площади с помощью палетки. Это может быть сделано в процессе такой беседы. Расчерчивать фигуру на квадратные сантимет­ры, говорит учитель, тоже довольно трудно. Для того чтобы облегчить задачу определения площади фигур, применяется прозрачная плен­ка, разделенная на квадратные сантиметры (палетка). Для нахождения площади фигуры достаточно наложить палетку на фигуру так, чтобы стороны квадратов на палетке совпали со сторонами фигуры. (Для демонстрации очень удобно использовать кодоскоп.) После показа палетки и измерения посредством ее площади фигуры учитель дает задание: изме­рить площади фигур 4 и 5, используя палетку. Учитель следит за тем, чтобы учащиеся пра­вильно накладывали палетку на фигуру.

Так как фигура 5 — прямоугольник, то при проверке задания проводится дополнительная работа, целью которой является подготовка к выводу правила вычисления площади прямо­угольника. Учащиеся под руководством учите­ля находят два рациональных способа подсче­та числа квадратов, содержащихся в прямо­угольнике. Можно также предложить уча­щимся измерить длину и ширину прямоуголь­ника и сравнить полученные числа с числом квадратных сантиметров в ряду и количеством рядов, с числом квадратных сантиметров в столбце и количеством столбцов. Здесь же проводится работа по предотвращению смешения учащимися понятии площадь прямоуголь­ника и периметр прямоугольника.

Дается задание: определить периметр пря­моугольника 5. Ставится ряд вопросов: что нужно сделать, чтобы найти площадь прямо­угольника? (Нужно разбить его на квадратные сантиметры и подсчитать их число.) Что нуж­но сделать, чтобы найти периметр прямоуголь­ника? (Нужно измерить его стороны и най­ти сумму длин всех сторон.) В каких едини­цах измеряется площадь? (В квадратных сан­тиметрах) . В каких единицах измеряется пери­метр? (В сантиметрах).

Для закрепления нового материала выпол­няются упражнения 382 и 383. При подведе­нии итога урока учитель еще раз подчеркива­ет все основные положения рассмотренного на уроке материала.

Вывод правила о вычислении площади пря­моугольника проводится так, как это описано в методических пособиях и в учебнике с не­большими, но очень важными, на наш взгляд, дополнениями. Вычисляя площадь прямоуголь­ника по правилу, необходимо подчеркивать, что, находя произведение чисел — значений длины и ширины прямоугольника, — мы фак­тически подсчитываем число квадратных сан­тиметров, содержащихся в нем. На первых уроках, а при затруднениях и на последую­щих, мы считаем необходимым требовать от учащихся словесного обоснования необходи­мости выполнения действия умножения над соответствующими числами для определения площади прямоугольника.

Это обоснование может выразиться в виде таких рассуждений.

Нам нужно, найти площадь в квадратных сантиметрах прямоугольника, длина которого равна 5 см, а ширина 4 см. Найти площадь прямоугольника — значит определить число квадратных сантиметров, помещающихся в нем. Длина данного прямоугольника 5 см, зна­чит, по его длине в одном ряду (полосе) уло­жится 5 квадратных сантиметров. Так как ши­рина прямоугольника 4 см, то таких рядов (полос) в нем будет 4, т. е. в прямоугольнике содержится 4 ряда по 5 квадратных сантимет­ров в каждом ряду. Тогда весь прямоуголь­ник содержит 5*4 кв. см, или 20 кв. см. Пло­щадь прямоугольника равна 20 кв. см. Анало­гичные рассуждения проводятся и для другого способа подсчета числа квадратов.

Не приводя здесь подробно хода урока по ознакомлению со способом вычисления площа­ди прямоугольника, отметим лишь последова­тельность формирования навыка вычисления площади прямоугольника.

Определение площадей прямоугольников, длина одной из сторон которых равна 1 см.

Определение площадей -прямоугольников, длины сторон которых более 1 см и выражают­ся натуральными числами, путем разбиения их на квадратные сантиметры одним из способов, затем путем разбиения на полосы или столб­цы шириной в 1 см и, наконец, с помощью нанесения только делений по длине и ширину.

Формулировка правила. Вычисление пло­щади прямоугольника путем нахождения про­изведения соответствующих чисел с обоснова­нием и последующей проверкой результата пу­тем разбиения прямоугольника на квадратные сантиметры палеткой или расчерчивания и не­посредственного их подсчета.

Выработка умения вычислять площадь прямоугольника по его длине к ширине. Обо­снование и непосредственное измерение тре­буется от учащихся лишь в случае затрудне­ния или при обнаружении ошибки.

Первый, второй и третий этапы в основном выполняются на одном уроке. Четвертый этап продолжается в течение всех последующих уроков до полного и осознанного овладения учащимися соответствующим умением.

Представленная здесь последовательность формирования умения вычислять площадь прямоугольника позволяет добиться прочности и осознанности его усвоения. Учащиеся получа­ют возможность проводить самоконтроль при выполнения заданий на определение площади прямоугольника.

Яркие, конкретные представления о смысле измерения площади, которые учащиеся полу­чают в процессе выполнения приведенных в статье упражнений, и выполнение в дальней­шем заданий на определение площади и пери­метра одного я того же прямоугольника пре­дупреждают смещение понятий площадь пря­моугольника и периметр прямоугольника. И са­мый важный результат при таком изучении площади прямоугольника — это исключение ме­ханического запоминания правила вычисления площади прямоугольника.

Использование палетки на первых этапах ознакомления с площадью позволяет подчер­кнуть общность понятия площади для всех фи­гур независимо от их формы. На уроке же, ко­торый посвящен измерению площади палет­кой (№ 397—399), учитель знакомит учащихся с приближенным вычислением площади фи­гур, показывает целесообразность применения для этого палетки. При этом в задания по определению приближенных значений площади можно включать также и прямоугольники, длины сторон которых не содержат целое число сантиметров.

Рассмотренный подход к изучению площа­ди исключает возможность ошибочного толко­вания различных способов измерения площа­ди. Учащиеся при необходимости могут обосновать определение площади прямоугольника через произведение соответствующих чисел, опираясь на общие представления о смысле измерения площади. Умение проводить такое обоснование позволяет контролировать себя при выполнении заданий, требующих нахож­дения площади прямоугольника и его пери­метра.