Разряд с осцилляцией электронов в магнитном поле и его инициирование, страница 5

Физический смысл возникновения двузначности функции u(b), по-видимому, тот же, что и у двузначности функции u(р) для разряда с полым катодом: в условиях, соответствующих нижней ветви, электроны сравнительно медленно движутся поперек  магнитного поля и успевают растратить почти всю свою энергию на ионизацию, а в условиях, соответствующих верхней ветви быстрые частицы обладают высокой энергией и могут осуществить большое число ионизаций, но они и быстрее диффундируют поперек магнитного поля и уходят на анод, успев растратить лишь незначительную часть своей энергии. Впрочем, как и для разряда с полым катодом, следует сказать, что качественный вид экспериментальных зависимостей U(B) соответствует нижней ветви приведенной зависимости, а, что касается верхней ветви, то такие растущие  зависимости наблюдались в экспериментах по зажиганию разряда [99], но автору не известны работы, в которых наблюдались бы такого рода зависимости для напряжения горения разряда. По - видимому, состояния, соответствующие верхней ветви являются неустойчивыми. В подтверждение этого можно провести рассуждения, полностью аналогичные тем, что были сделаны в главе 2 при анализе двузначности функции u(p).

Выполнение условия самостоятельности является необходимым, но не достаточным условием для реализации рассматриваемой формы разряда. Необходимо еще выяснить при каких условиях квазинейтральная плазма будет заполнять весь промежуток от прикатодного ионного слоя до анода и вблизи анода не появится электронный слой. Пренебрегая вкладом быстрых частиц в полный отрицательный заряд запишем условие квазинейтральности в виде

                n_e = n_i =n.                                                                  (4.2.22)

При найденной функции n_f(x) решение системы уравнений (4.2.8)-(4.2.11), (4.2.22) не вызывает особых затруднений. Для плотностей электронного и ионного потоков получается соответственно

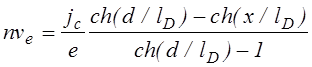,                                     (4.2.23)

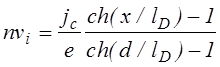.                                                     (4.2.24)

Для определения концентрации плазмы комбинируем уравнения (4.2.10) и (4.2.11) и избавляясь от членов, содержащих dj/dx, получаем после некоторых преобразований следующее уравнение

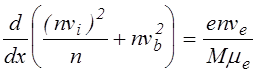.                                               (4.2.25)

Проинтегрируем записанное уравнение в пределах от некоторой точки х до границы между плазмой и ионным слоем, при этом пренебрегаем толщиной катодной области и считаем, что эта граница находится в точке ,

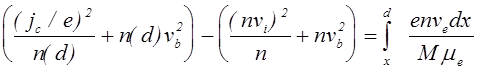.         (4.2.26)   

Разрешая полученное выражение относительно n получаем

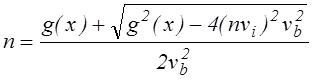,                                     (4.2.27)

где

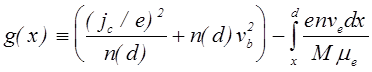.                            (4.2.28)

Полученная формула (4.2.27) имеет физический смысл лишь тогда, когда выражение, стоящее под знаком квадратного корня, положительно, а точки в которых это выражение обращается в 0 являются границами квазинейтральной плазмы. Одна из таких точек это граница между плазмой и прикатодным слоем. Учитывая, что f(d)=0 и nv_i(d)=j_c/e, получаем

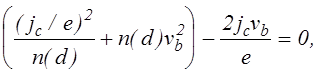                                     (4.2.29)

откуда для концентрации плазмы на границе с прикатодным ионным слоем находим

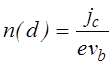.                                                                       (4.2.30)

Поскольку нас интересует случай когда плазма заполняет весь газоразрядный промежуток от прикатодного слоя до анода, то во всем остальном промежутке подкоренное выражение должно быть положительным и лишь в крайнем случае оно может обратиться в 0 на аноде. Учитывая, что ионный ток на аноде равен нулю, а концентрация не может быть отрицательной, получаем, что для реализации рассматриваемой формы разряда необходимо выполнение условия , что обеспечивается, если

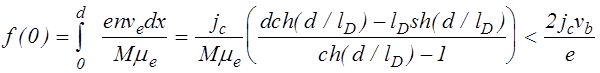  (4.2.31)

Учитывая, что коэффициент подвижности электронов поперек магнитного поля пропорционален концентрации нейтрального газа N можно преобразовать (4.2.31) к следующему виду

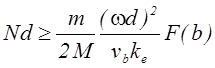,                                                         (4.2.32)