Разряд с осцилляцией электронов в магнитном поле и его инициирование, страница 11

4.4.1. Движение электронов в электрическом и магнитном полях

Электроны, эмиттированные катодом, начинают под действием электрического поля движение к аноду. Магнитное поле отклоняет их и в результате электроны, не испытавшие при первом пролете через полость ни одного столкновения, подлетают к нему с той же энергией, которая имелась в момент вылета из катода, и могут либо отразиться от поверхности катода либо поглотиться ею. В последнем случае с некоторой вероятностью может произойти вторичная электрон-электронная эмиссия. Следует отметить, что отраженные электроны также часто рассматривают как вторичные и вводят в рассмотрение эффективный коэффициент вторичной эмиссии d*, равный сумме вероятностей "истинной" вторичной эмиссии и отражения. Поскольку никакой существенной разницы между истинно вторичными и отраженными электронами нет, то будем считать, что g - электрон, пролетевший через полость без столкновений после взаимодействия с поверхностью с вероятностью d* продолжает  движение и, соответственно, с вероятностью (1-d*) поглощается катодом. Аналогичная ситуация возникает после второго, третьего и т.д. пролета через полость. Если же электрон во время движения через полость испытал столкновение и потерял часть своей энергии, то он уже не достигнет поверхности катода и не будет ею поглощен. Обозначив вероятность испытать столкновение в течение одного пролета через полость через Р_с  можно для вероятности возврата электрона на катод записать следующее выражение

P_b=(1-P_c)(1-d*)+(1-P_c)²d*(1-d*)+(1-P_c)³d*²(1-d*)+...    (4.4.1)

Первый член в правой части уравнения (4.4.1) есть вероятность вернутся на катод после первого пролета через полость, второй член дает  вероятность  поглощения после второго пролета и т.д. Вынося (1-P_c)(1-d*) за скобки преобразуем (4.4.1) к виду

P_b = (1-P_c)(1-d*)(1+(1-P_c)d* +(1-P_c)²d*²+...)                   (4.4.2)

из которого видно, что выражения в скобках представляют собой геометрическую прогрессию с коэффициентом q=(1-P_c)d*. Используя выражение для суммы членов геометрической прогрессии получаем для вероятности ухода на катод следующее выражение

P_b = 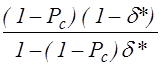                                                         (4.4.3)

Вероятность столкновения за время одного пролета через полость можно рассчитать используя следующее выражение

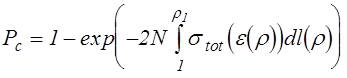,                                  (4.4.4) где  - точка поворота траектории электрона (точка, в которой радиальная составляющая скорости меняет знак), - полное сечение рассеяния, то есть сумма сечений ионизации, возбуждения и упругого рассеяния. Множитель 2 появился вследствие симметрии траектории относительно точки поворота. Поскольку относительно полного  сечения имеются достаточно надежные экспериментальные данные, то коэффициент Р_с можно рассчитать с хорошей точностью. К сожалению этого нельзя сказать о коэффициенте d*,  данные о котором скудны и противоречивы, что, по - видимому, связано с тем обстоятельством, что на вероятность вторичной электрон-электронной эмиссии существенно влияет состояние поверхности [101]. В связи с этим коэффициент d* рассматривался при расчетах как подгоночный параметр и его значение варьировалось в пределах от 0 до 1.

Непоглощенные электроны постепенно движутся к аноду, испытывая по пути упругие и неупругие, в том числе ионизационные столкновения. Аналогичным образом ведут себя вторичные электроны, они тоже могут образовывать новые заряженные частицы путем ионизации, пока не уйдут на анод. Уход вторичных электронов на катод невозможен, так как они не имеют достаточной для этого энергии.  Так происходит до тех пор, пока все электроны не покинут разрядную камеру. В результате электронного размножения в разрядной камере появляется некоторое число ионов N_i, которые под действием электрического поля устремляются к катоду. При взаимодействии с катодной поверностью каждый ион образует g электронов и в результате для коэффициента электронного размножения mполучаем