Разряд с осцилляцией электронов в магнитном поле и его инициирование, страница 12

                                                                           (4.4.5)

Коэффициент вторичной ион - электронной эмиссии стали рассчитывался по эмпирической формуле

,                                    (4.4.6)

предложенной в [80], где - работа выхода.

Очевидно, что для развития самостоятельного разряда необходимо выполнение условия

.                                                                (4.4.7)

Конфигурация электродов и наличие в системе магнитного поля налагает свои особенности на процесс зажигания. Во-первых, коэффициент электронного размножения зависит теперь ещё и от индукции магнитного поля, а во-вторых, становится существенным, как уже отмечалось выше, процесс ухода первичных электронов на катод. Для учета этого процесса вводился эффективный коэффициент вторичной эмиссии

.                                                      (4.4.8)

При сделанных допущениях относительно электродной геометрии распределение потенциала в промежутке между двумя коаксиальными  цилиндрами описывается простой аналитической зависимостью

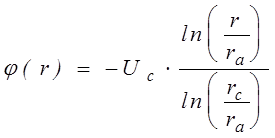,                                           (4.4.9)

где  r_c  - радиус катода, а r_a - радиус анода, потенциал анода принят равным нулю, а потенциал катода равен -U_c. Уравнения движения заряженной частицы в электрическом и магнитном полях в общем случае приведены в работе [102]. Для рассматриваемой задачи с однородным продольным магнитным полем в цилиндрической системе координат (r, f, z) они существенно упрощаются и принимают следующий вид:

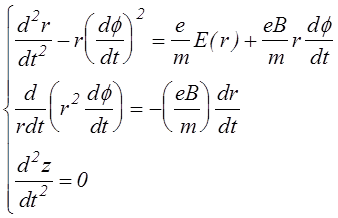             .(4.4.10)

Введем некоторые обозначения и перейдем к безразмерным величинам в уравнениях движения. Второе уравнение системы (4.4.10) можно преобразовать к следующему виду

= 0.                                                  (4.4.11)

При такой форме записи становится очевидным, что величина  является интегралом движения, который в дальнейшем будем обозначать через . Вводя также обозначения

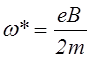,                                                                          (4.4.12)

,                                                              (4.4.13)                                      

и

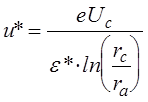                                                                  (4.4.14) перейдем к безразмерным переменным

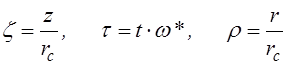                                           (4.4.15)

и интегрируя уравнения (4.4.11), получим следующую систему:

 (4.4.16)

где r₀ - начальная координата частицы, а

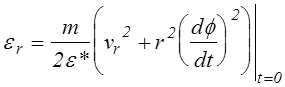                                            (4.4.17)

это начальная кинетическая энергия радиального движения, отнормированная на e*. Выражение для элементарного отрезка пути   электрона   в безразмерных переменных выглядит следующим образом:

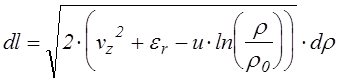.                                (4.4.18)

4.4.2.  Элементарные процессы

При анализе столкновений электронов рассматривались процессы однократной ионизации, возбуждения первого электронного уровня и упругие столкновения. Процессы двукратной, трехкратной и т. д. ионизации,  процесс рекомбинации и процессы возбуждения 2-го, 3-го и т. д. электронных уровней не учитывались так как их вероятность мала по сравнению с вышеперечисленными процессами При рассмотрении процессов ионизации, возбуждения и упругого столкновения принималось, что атомы аргона неподвижны. Это приближение вполне допустимо в силу большого различия масс атома и электрона.

Для расчета  сечений ионизации и возбуждения использовалисьть приближенные формулы, приведенные в работе [103]:

                     (4.4.19)

где

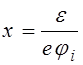,                                                                           (4.4.20)

и

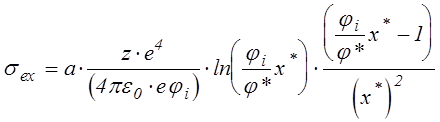                (4.4.21)

где

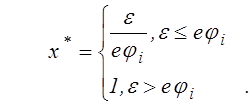                                                         (4.4.22)

В записанных выражениях использованы также следующие обозначения:  - заряд атома аргона, j*=14.55 эВ - энергия возбуждения первого электронного уровня,  - поправочный коэффициент. При учете упругого взаимодействия использовались экспериментальные данные, приведенные в работе [104], которые аппроксимировались следующими формулами: