Разряд с осцилляцией электронов в магнитном поле и его инициирование, страница 3

где n_f, v_f - концентрация и средняя скорость  направленного движения быстрых частиц поперек магнитного поля. В правой части (4.2.1) нет знака минус, так как за положительное направление для потоков как быстрых, так и медленных электронов будем считать направление от катода к аноду. Поток быстрых частиц определяется диффузией поперек магнитного поля

               n_fv_f = D_f ,                                                              (4.2.2)

где D_f - коэффициент диффузии, а дрейфовой составляющей можно пренебречь, так как слабое электрическое поле, имеющееся в плазме, не оказывает существенного влияния на движение быстрых частиц. Это было показано в главе 1 для случая разряда с полым катодом без магнитного поля. Убедимся, что это предположение остается справедливым и при движении быстрых электронов поперек магнитного поля. Оценим отношение характерного расстояния l, проходимого быстрым электроном в результате дрейфа за время релаксации, к характерной диффузионной длине l_D, определяемой следующим соотношением 

          l_D  = .                                                                     (4.2.3)

Для подвижности быстрых электронов можно записать следующее соотношение

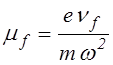,                                                                       (4.2.4)

где n_f - эффективная частота  столкновений для быстрых электронов,  w - ларморовская частота электрона. В (4.2.4) учтено, что для замагниченных электронов . Учитывая также, что квадрат скорости быстрой частицы меняется от 2eU_c/m, где U_c - катодное падение, практически до 0 и в среднем составляет величину ~ eU_c/m, запишемдля коэффициента диффузии быстрых частиц  следующее выражение

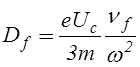.                                                                    (4.2.5)

Перепад потенциала на плазменной области рассматриваемых разрядов составляет величину порядка kT_e/e. Поскольку протяженность катодного слоя, как правило, существенно меньше размера плазменной области, то среднюю напряженность электрического поля в плазме можно оценить как

.                                                                              (4.2.6)

Используя (4.2.4) - ( 4.2.6) получаем

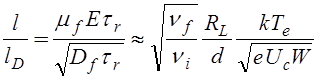,                                     (4.2.7)

где R_L ~ /w - характерный Ларморовский радиус быстрых электронов. В (4.2.7) отношение l/l_D представлено в виде произведения трех сомножителей, первый их которых  является величиной порядка единицы, второй R_L/d  для рассматриваемого разряда обязательно меньше единицы, так как в противном случае электроны сразу уйдут на анод и никаких осцилляций не будет, и наконец треттий сомножитель kT_e / являтся величиной много меньше единицы, так как тепловая энергия плазменных электронов существенно меньше и энергии быстрых частиц  и энергетической цены иона.Таким образом и в целом рассматриваемое отношение является величиной много меньше единицы, а значит дрейфовой составляющей потока быстрых частиц можно пренебречь по сравнению с диффузионной.

Для потока плазменных электронов существенными являются и диффузионная и дрейфовая составляющая

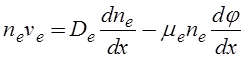,                                                (4.2.8)

где n_e, v_e, D_e и m_e - концентрация, средняя скорость направленного движения, коэффициент диффузии и коэффициент подвижности медленных электронов в поперечном магнитном поле, а j - потенциал. Уравнение непрерывности для медленных частиц запишем в следующем виде

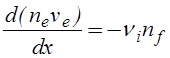.                                                             (4.2.9)

Для большей точности в правую часть (4.2.9) следовало бы добавить член, соответствующий переходу электронов из группы быстрых частиц в группу медленных, но он существенно меньше ионизационного члена и им можно пренебречь. Что касается уравнения непрерывности для ионов, то оно выглядит аналогично

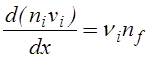,                                                                (4.2.10)