Разряд с осцилляцией электронов в магнитном поле и его инициирование, страница 2

При проведении экспериментов использовались такие широко известные системы с осцилляцией электронов как Прямой и Обращенный Магнетроны и Пеннинговская Система, изображенные на рис. 4.1 - 4.3, соответственно. Использовался тот же набор электродов, что и в экспериментах по изучению тлеющего разряда с полым катодом, описанных в 2.1, и кроме того снаружи разрядной камеры соосно с ней устанавливался соленоид. Переход от одной системы к другой осуществлялся за счет подсоединения стержневого и цилиндрического электродов к различным полюсам источника питания. На торцевые электроды подавался отрицательный (катодный) потенциал. Следует отметить, что в  магнетронных системах торцевые электроды могут также находиться под анодным или под плавающим потенциалом, что применяется достаточно широко, но в этих случаях, как показали предварительные эксперименты, для

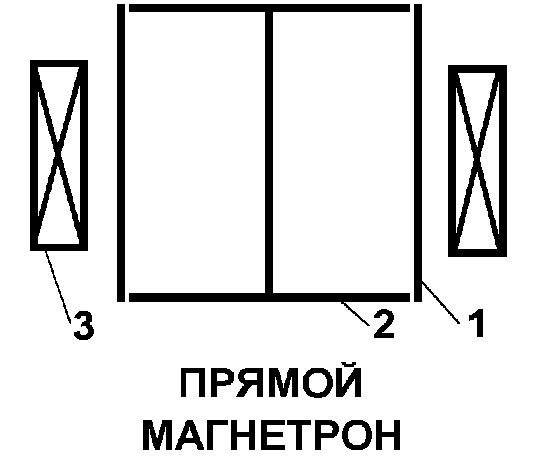
Рис. 4.1. 1 - анод, 2 - катод, 3 - соленоид.

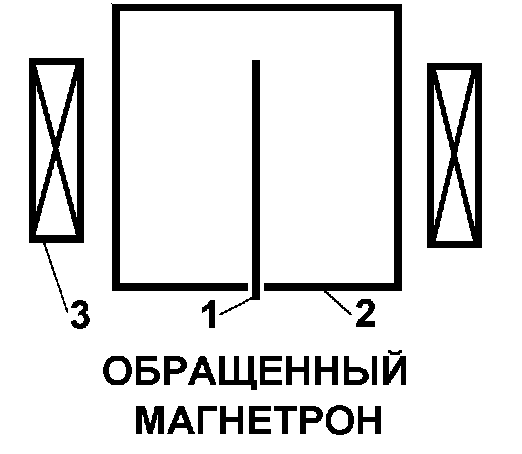
Рис. 4.2. 1 - анод, 2 - катод, 3 - соленоид.

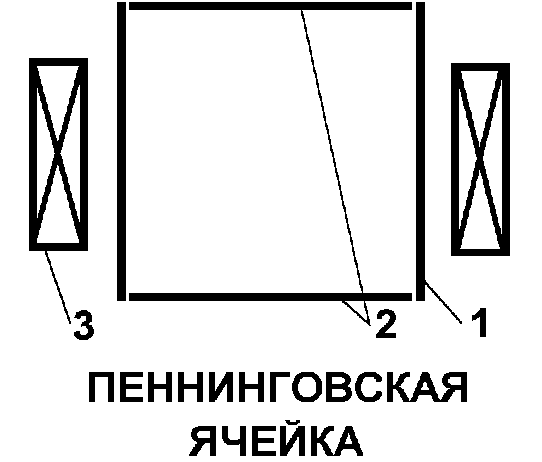
Рис.4.3. 1 - анод, 2 - катод, 3 - соленоид.

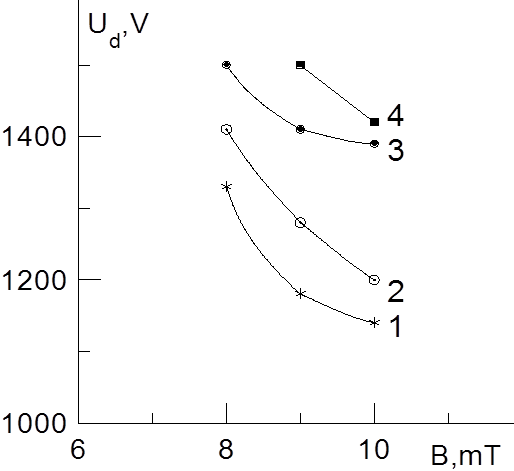
Рис. 4.4. Прямой магнетрон. р (мПа): 1- 36, 2 - 27, 3 - 22, 4 - 18

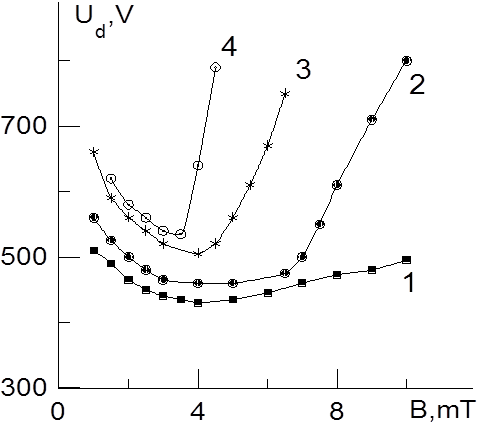
Рис. 4.5. Обращенный магнетрон. р (мПа): 1- 18, 2 - 13, 3 - 9, 4 - 7

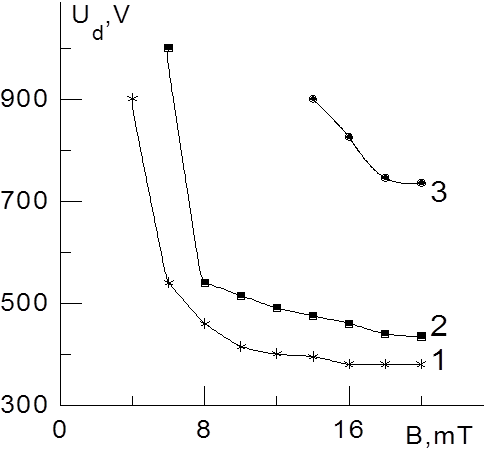
Рис. 4.6. Пеннинговская система. р (мПа): 1- 32, 2 - 16, 3 - 9

горения разряда необходимо резкое, больше чем на порядок, увеличение давления по сравнению со случаем, когда торцы имели катодный потенциал, и в дальнейшем исследовался только этот случай.

На рис 4.4 - 4.6 приведены экспериментальные зависимости напряжения горения разряда от индукции магнитного поля, снятые при различных давлениях. Сравнивая полученные характеристики разрядов в магнитном поле и приведенные во второй главе характеристики разрядов с полым катодом, можно сделать вывод, что при прочих равных условиях наиболее низкое рабочее давление достигается в системе типа обращенный магнетрон.

Как видно из приведенных рисунков при использовании системы типа обращенный магнетрон зависимости являются немонотонными, причем растущие участки зависимостей U_d(B) смещаются в область более сильных магнитных полей с увеличением давления. Что же касается Пеннинговской ячейки и системы типа прямой магнетрон, то здесь в исследованном диапазоне параметров с увеличением индукции магнитного поля наблюдалось монотонное уменьшение напряжения горения. Для объяснения полученных результатов была разработана аналитическая модель разряда в магнитном поле, описываемая в следующем параграфе.

4.2 Модель разряда в магнитном поле

Рассмотрим задачу в плоской геометрии. Будем считать, что в плоскости х=0 расположен анод, а в плоскости х=d катод газоразрядной системы. Как правило, влиянием магнитного поля на движение ионов, обладающих большой массой, можно пренебречь. Кроме того при низких давлениях в Кнудсеновском режиме разряда можно считать, что ионы покидают промежуток без столкновений. Что же касается электронов, то в рассматриваемых разрядах они, как правило, являются замагниченными и вследствие осцилляций в магнитном поле проходят путь, существенно превышающий длину промежутка. Следовательно, при рассмотрении движения электронов несмотря на формальное выполнение  условий Кнудсеновского режима учет столкновений необходим.

Учитывая, что оба рассмотренных в главе 2 при анализе разряда с полым катодом случая (n_i~const, s_i~const)дают близкие результаты, а также то, что допущение n_i~const (s_i~1/v) более точно соответствует ходу экспериментальных зависимостей сечения ионизации в характерном для быстрых частиц диапазоне энергий, ограничимся для разряда в магнитном поле анализом только этого случая. Считая, что по истечении времени релаксации t_r  быстрая частица утрачивает способность к ионизации и переходит в группу медленных частиц,   запишем уравнение непрерывности для быстрых частиц в следующем виде

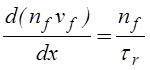,                                                              (4.2.1)