Исследование типовых динамических звеньев (Лабораторная работа № 5)

Лабораторная работа 5

Исследование типовых динамических звеньев

3.1. Цель работы

Закрепить материал лекций по свойствам    типовых динамических звеньев. Приобрести навыки исследования этих звеньев с помощью системы СИАМ.

3.2. Задание на выполнение лабораторной работы

1.  Отработать навыки  решения задач по исследованию свойств звеньев САР на основе их дифференциальных уравнений, передаточных и переходных функций.

2.  С помощью системы СИАМ рассчитать на ПЭВМ переходные функции звеньев:

-  интегрирующего;

-  апериодического;

-  колебательного.

3.  По таблицам и графикам переходных функций звеньев определить параметры их передаточных функций.

4.  Сделать выводы по результатам исследований.

3.3. Методические указания

1.  Повторить особенности исследования САУ с использованием системы СИАМ в режимах:

-  набора модели;

-   вычисления временных характеристик и вывода результатов в     виде таблиц и графиков;

2.  Для получения допуска к выполнению лабораторной работы по конспекту лекций и рекомендованной литературе подготовиться к ответам на следующие вопросы:

а) что называется звеном АС?

б) какие передаточные и переходные функции имеют следующие звенья:

-   простое усилительное;

-   идеальное интегрирующее;

-   идеальное дифференцирующее;

-  апериодическое (инерционное 1-го порядка);

-  колебательное;

-    чистого запаздывания?

в)  как по графикам переходных функций определить параметры передаточных функций усилительного, идеального интегрирующего, апериодического, колебательного?

3.4. Краткие теоретические сведения

Звеном называется часть САУ, оператор которой описывается   дифференциальным уравнением не выше 2-го порядка. Классификация звеньев по виду их передаточных функций представлена в таблице 3.1. Здесь  k – коэффициент усиления,T – постоянная времени,  x - относительный коэффициент затухания звена. Для определения параметров звена по виду его передаточной функции последняя обязательно должна быть приведена к стандартному виду, например:

   , это апериодическое звено, его коэффициент усиления k =5,  постоянная времени T=1.5 с;

3.5. Решение задач по свойствам звеньев

Задача 1.   Дано: передаточная функция звена САУ

.

Требуется определить тип звена и его параметры: коэффициент усиления, постоянную времени и относительный коэффициент затухания.

Решение:

Приводим передаточную функцию звена к стандартному виду:

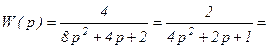
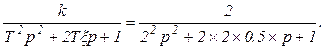
Это колебательное звено, его коэффициент усиления k=2,  постоянная времени T=2 с,  относительный коэффициент затухания x=0.5.

Предлагается самостоятельно решить эту же задачу для следующих вариантов:

1)    ,      

2)    ,    

3)    .

Ответы:

1) форсирующее звено первого порядка,     k = 3,  T = 2 c.

2) апериодическое звено,        k =0.25,  T = 0.5 c.

3)  колебательное звено,           k =0.5,  T = 1 c, x = 0.5.

Задача 2. Дано: передаточная функция звена САР

 и входной сигналx(t)= 1(t).

Требуется определитьвыходной сигналy(t).

Решение:

1)  По табл.3.2. определяем изображение по Лапласу входного сигнала:

Таблица 3.1.

№               Передаточная                                Название звена

    п/п             функция  звена                         

1                                                                       усилительное

2                                                         идеальное дифференцирующее

3                                                                    интегрирующее   

4                                                форсирующее 1-го порядка 

5                            форсирующее 2-го порядка

апериодическое                                                            (инерционное 1-го порядка)

     6                                                                 

инерционное  2-го порядка:                                                       -  колебательное;  -  апериодическое 2-го          порядка;    -  консервативное;   -  неустойчивое.

                     7                             

8                                                  звено чистого запаздывания            

реальное дифференцирующее (изодром)

                         

9                                                

апериодическое с введением производной

    10                                                   

 

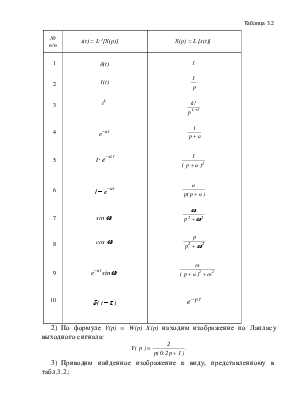
Таблица 3.2

№ п/п	x(t) = L-1[X(p)]	X(p) = L [x(t)]
1 2 3 4 5 6 7 8 9 10	d(t) 1(t) tk       sin wt cos wt	1

2)  По формуле Y(p) = W(p) X(p)находим изображение по Лапласу выходного сигнала:

3)  Приводим найденное изображение к виду, представленному в табл.3.2.:

4)  По табл.3.2. определяем выходной сигнал y(t) = L^-1[X(p)]: