Исследование типовых динамических звеньев (Лабораторная работа № 5), страница 2

Предлагается самостоятельно решить эту же задачу для вариантов, представленных в табл. 3.3.

Таблица 3.3.

Вар.№	Дано:		Ответ:
	W(p)	x(t)	y(t)
1 2 3 4 5	5 3×p	1(t) 1(t) 1(t) d(t) d(t)	5 ×1(t) 3×d(t) 10×t

Задача 3. Дана переходная функция звена (см. рис.3.1)

Требуется определить передаточную функцию звена и его параметры.

Решение:

Переходной функцией звена h(t)называется ее реакция на

 

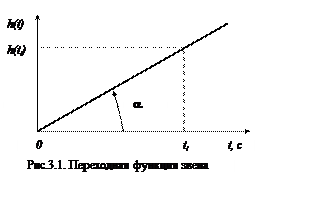единичный ступенчатый сигнал. По таблице графиков переходных функций типовых звеньев определяем, что это переходная функция интегрирующего звена. Его передаточная и переходная функцииопределяются формулами:

,           .

Коэффициент усиления интегрирующего звена определяется по формуле

.                           (3.1)

Задача 4.Дана переходная функция звена (см. рис.3.2)

Требуется определить передаточную функцию звена и его параметры.

Решение:

Такой вид имеет график переходной функции апериодического звена. Его передаточная  и переходная функцииопределяются формулами:

,        .

Нетрудно убедиться, что коэффициент усиления апериодического звена определяется по формуле    

.                                    (3.2)

Постоянную времени звена при использовании СИАМ проще определить по формуле  T»t_Р / 3,  где  t_Р - время регулирования.

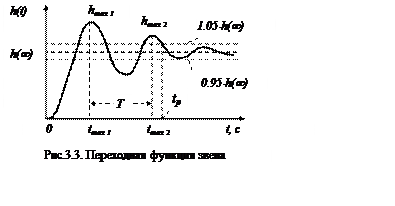
  Задача 5. Дана переходная функция звена (см. рис.3.3).

 

Требуется определить передаточную функцию звена и его  параметры.

Решение:

Такой вид имеет график переходной функции колебательного звена. Его передаточная  функция имеет вид:

                 (3.3)

0<x<1,                 W₀=1/T₀.

Корни характеристического уравнения  звена

,                  (3.4)

равны                          , где         ,   ,   .   

Переходная функция звена, определенная на основании теоремы разложения с использованием корней уравнения (3.4), имеет вид:

,                        (3.5)

где      .  

Его коэффициент усиления, как и у апериодического, определяется по формуле

.                                      (3.6)

Измерив расстояние по оси времени между двумя любыми соседними максимумами, можно найти период вынужденных колебаний  T =t_max2 - t_max1  и, следовательно, и угловую частоту этих колебаний:

.                                              (3.7)

Как известно,

t_max1 = T/2 = p/wили       T = 2t_max1.               (3.8)

На практике для определения периода колебаний T удобнее  пользоваться именно этой формулой. С ее использованием несложно получить следующую зависимость:

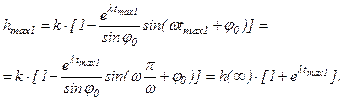
Отсюда определяем

,    где       .            (3.9)

Зная действительную  lи мнимую  wчасти корней уравнения (3.4), можно вычислить искомые параметры передаточной функции (3.3):

;            .                  (3.10) 

3.6.  Порядок выполнения работы

1) Войти в СИАМ,  набрать структурную схему исследования интегрирующего звена где его коэффициент усиления  kзадать в соответствии с предложенными преподавателем вариантами из таблицы 3.4.

Таблица 3.4.

Вар.№	1	2	3	4	5	6	7	8	9
k	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0	9.0
tk, с	10	10	10	10	10	10	10	10	10