Лабораторная работа №6
Определение передаточных функций САУ
c помощью ЭВМ
2.1. Цель работы
Закрепить материал лекций по определению передаточных функций САУ. Приобрести навыки вычисления передаточных функций САУ с помощью системы СИАМ.
2.2. Задание на выполнение лабораторной работы
1. Отработать навыки решения задач по определению передаточных функций САУ на основе их дифференциальных уравнений и структурных схем.
2. Изучить особенности определения передаточных функций САУ с помощью СИАМ.
3. Определить аналитически передаточную функцию САУ, заданную преподавателем, набрать ее структурную схему на
ЭВМ и определить передаточную функцию с помощью СИАМ.
4. Сделать выводы по результатам проведенных исследований.
2.3. Методические указания
1. Повторить особенности исследования САУ с использованием системы СИАМ в режимах набора модели, определения передаточных функций.
2. Для получения допуска к выполнению лабораторной работы по конспекту лекций подготовиться к ответам на следующие вопросы:
а) что называется передаточной функцией, характеристическим уравнением, нулями и полюсами САУ?
б) чему равно изображение по Лапласу производной k-го порядка?
в) как определить передаточную функцию САУ на основе дифференциального уравнения?
г) по каким формулам вычисляются передаточные функции последовательного, параллельного и встречно-параллельного соединений звеньев?
2.4. Краткие теоретические сведения
Передаточная функция, характеристическое уравнение САУ
Передаточной функцией линейной стационарной САУ называется отношение изображения по Лапласу выходного сигнала Y(p)к такому же изображению входного сигнала X(p)при нулевых начальных условиях:
![]() .
.
Передаточная функция отражает передающие свойства САУ, поэтому при ее определении с целью упрощения исследований предполагается, что до начала воздействия входного сигнала САУ находится в покое.
Для определения W(p)необходимо записать оператор линейной стационарной САУ, заданный в виде дифференциального уравнения:
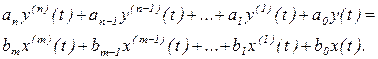
В левой части этого уравнения обычно пишут оператор выходного сигнала, в правой - оператор входного сигнала. Исследование дифференциальных уравнений существенно упрощается, если их преобразовать с помощью преобразования Лапласа. Напомним формулы преобразования Лапласа производных при нулевых начальных условиях:
L[y(t)] = Y(p); L[y(1)(t)] = pY(p); L[y(2)(t)] = p2Y(p), …
L[x(t)] = X(p); L[x(1)(t)] = pX(p); L[x(2)(t)] = p2 X(p), … .
Применив преобразование Лапласа к правой и левой части дифференциального уравнения, получим его операторную форму записи:
![]()
тогда в соответствии с видом этого оператора
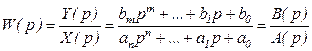 .
.
Таким образом, ПФ является дробно-рациональной функцией комплексной переменной преобразования Лапласа p, она не зависит от входного сигнала, а определяется структурой и параметрами САУ.
Знаменатель передаточной функции A(p)называется характеристическим, а уравнение
![]() , называется характеристическим
уравнением САУ.
, называется характеристическим
уравнением САУ.
Корни характеристического уравнения pi, где ![]() , называются полюсами
передаточной функции. Для наглядности их принято изображать на комплексной
плоскости. Распределение полюсов на комплексной плоскости характеризует основные
свойства САУ.
, называются полюсами
передаточной функции. Для наглядности их принято изображать на комплексной
плоскости. Распределение полюсов на комплексной плоскости характеризует основные
свойства САУ.
Корни числителя передаточной функции
![]() , называются ее нулями.
Определение и исследование передаточной функции и характеристического уравнения
занимают центральное место в ТАУ.
, называются ее нулями.
Определение и исследование передаточной функции и характеристического уравнения
занимают центральное место в ТАУ.
Определение передаточных функций САУ методом преобразования структурных схем
Одним из основных методов исследования САУ является метод преобразования структурных схем.
Структурной схемой САУ называется графическое изображение ее элементов, представленных своими переда-точными функциями, и связей между ними.
Передаточная функция последовательного соединения звеньев САУ
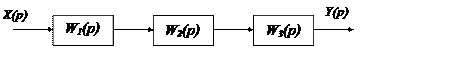 |
![]()
Т.е. ПФ последовательного соединения звеньев САУ равна произведению их ПФ:
Передаточная функция параллельного соединения звеньев САУ
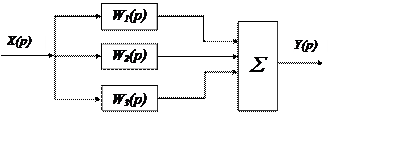 |
![]()
Т.е. ПФ параллельного соединения звеньев равна сумме их ПФ.
Передаточная функция встречно-параллельного соединения звеньев САУ с отрицательной обратной связью
![]()
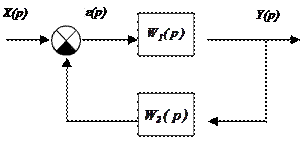 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.