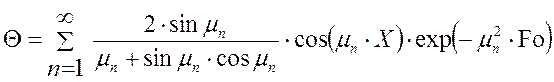Общие сведения о нагреве металла. Пример расчета нагрева металла в четырехзонной методической печи, страница 4

,         где  – корни характеристического уравнения 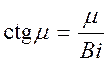;  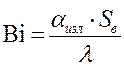– число Био;  – безразмерная координата ( – для центра пластины,  – для поверхности пластины); 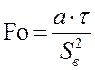 – число Фурье.

Если число Фурье , то ряд становится настолько быстросходящимся, что распределение температуры достаточно точно описывается его первым членом:

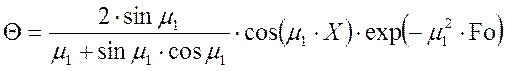,.                     (5)

где .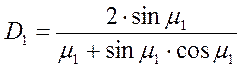

Первый корень характеристического уравнения для неограниченной пластины определяется по формуле:

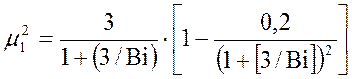.                                           (6)

Из формулы (5) можно определить безразмерный критерий Фурье:

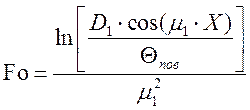,                                        (7)

тогда время нагрева металла в отдельной зоне определяется как:

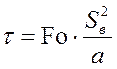.                                                             (8)

Средняя по сечению температура металла (безразмерная):

.

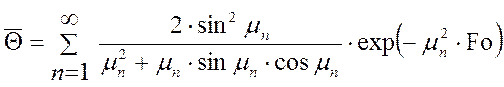Если число Фурье , то ряд становится настолько быстро сходящимся, что распределение температуры описывается его первым членом.

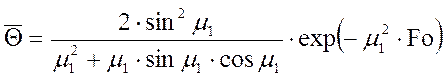.                             (9)

Значение средней по сечению температуры металла определяется в соответствии с формулой (4) как:

,                                                 (10)

где  – значение средней по сечению температуры металла в начале зоны.

При расчёте томильной зоны необходимо учесть особенности нагрева в ней. Так как в томильной зоне температуры среды и поверхности металла равны, то следует принять значение коэффициента теплоотдачи . Безразмерный критерий Био прямо пропорционален , следовательно, тоже . Получаем предельный случай, в котором формула для нахождения безразмерной температуры  принимает следующий вид:

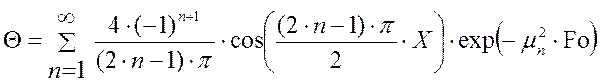, так как корни характеристического уравнения в случае  определяются по формуле: .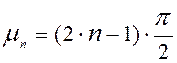

Если число Фурье , то ряд становится настолько быстро сходящимся, что распределение температуры достаточно точно описывается его первым членом:

.

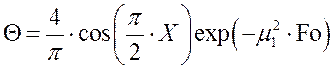Первый корень характеристического уравнения равняется 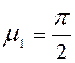, тогда безразмерная температура для центра пластины определяется как:

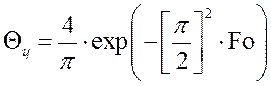, а безразмерный критерий Фурье определяется по формуле:

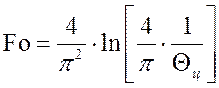.                                      (11)

1.2. Определение коэффициента теплоотдачи излучением

Необходимый для расчёта числа Био коэффициент теплоотдачи  рассчитываем на основе закона Ньютона – Рихмана. По определению коэффициент теплоотдачи равен отношению плотности теплового потока к разности температур между стенкой (поверхностью металла) и жидкой средой (дымовыми газами):

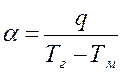.                                                    (12)

Собственное излучение газа и поверхности металла определяется на основе закона Стефана – Больцмана, а искомая плотность теплового потока определяется как результирующий поток между газом и металлом:

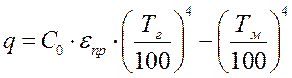,                                            (13)

где  Вт/(м^2.К⁴) – коэффициент излучения абсолютно черного тела.

Тогда, на основании формул (12) и (13), коэффициент теплоотдачи излучением будет равен:

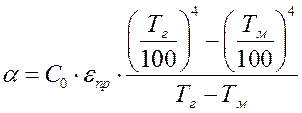.                                          (14)

Приведённый коэффициент излучения в системе газ – кладка – металл определяется по формуле:

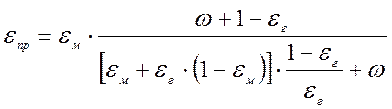,                                (15)

где  – степень черноты углеродистых и легированных конструкционных марок сталей;  – степень черноты продуктов сгорания; w – степень развития кладки печи.

Степень черноты продуктов сгорания определяется по формуле:

.                                                   (16)

Значения поправочного коэффициента , степени черноты углекислого газа  и водяных паров , содержащихся в продуктах сгорания, находят по номограммам (см. рис. 3–5). Для этого необходимо рассчитать парциальное давление излучающих газов ,  и параметр , где  – эффективная длина пути луча. Затем по значению температуры среды (дымовых газов) или стенки (поверхность металла) и параметру  определяют соответствующие значения степеней черноты излучающих газов.

Парциальное давление излучающих газов определяется из выражений:

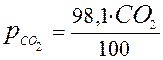,                                                        (17)