Глава II. Гидромеханические явления процесса
формирования отливок
Гидромеханические явления поведения металлических расплавов рассматриваем как приложения законов гидростатики и гидродинамики к анализу технологических операций, связанных с жидким металлом. Гидромеханические явления рассматриваются для металлов и сплавов с перегревом 20-100°С и выше над температурой затвердевания, при котором металлические расплавы ведут себя как обычные капельные (ньютоновские) жидкости.
2.1. Приложения законов гидростатики к поведению
расплавов металлов в литейных печах, ковшах,
разливочных устройствах, литейных формах
Величина давления расплава на дно ковша, литейной формы описывается выражением:
![]() , где r – плотность расплава;
g – ускорение земного притяжения; h – высота столба жидкого металла; р0 –
величина давления на свободную поверхность расплава, чаще всего р0
= ратм – атмосферному давлению. Но в некоторых практических
случаях литейных технологий р0 ¹
ратм. Например, в вакуумных печах, литейных формах,
заливаемых вакуумным всасыванием или под разрежением р0 < ратм.
И напротив в герметизированных ковшах при модифицировании чугуна магнием в
автоклавном способе литья р0 > ратм.
, где r – плотность расплава;
g – ускорение земного притяжения; h – высота столба жидкого металла; р0 –
величина давления на свободную поверхность расплава, чаще всего р0
= ратм – атмосферному давлению. Но в некоторых практических
случаях литейных технологий р0 ¹
ратм. Например, в вакуумных печах, литейных формах,
заливаемых вакуумным всасыванием или под разрежением р0 < ратм.
И напротив в герметизированных ковшах при модифицировании чугуна магнием в
автоклавном способе литья р0 > ратм.
По величине рассчитанного давления рд, определяем силу Р, действующую на отрыв дна ковша, на разрушение литейной формы в самой нижней ее части:
![]() , где F – площадь плоской поверхности
дна ковша (литейной формы).
, где F – площадь плоской поверхности
дна ковша (литейной формы).
Если полость литейной формы, полость ковша или печи имеет непостоянное по высоте поперечное сечение, то в расчетах следует учитывать известный гидростатический парадокс и вместо величины металлостатического rgh принимать величину силы тяжести жидкого металла, находящегося в емкости – Mg, где М – масса жидкого металла.
Величина силы давления, действующей на боковую поверхность литейной формы, ковша, печи определяется:
![]() , где Fб – площадь проекции
боковой поверхности литейной формы (ковша, печи); рб –
расчетная величина давления расплава на боковую поверхность:
, где Fб – площадь проекции
боковой поверхности литейной формы (ковша, печи); рб –
расчетная величина давления расплава на боковую поверхность: ![]() ,
, ![]() , т.е.
половина величины металлостатического напора. По величине силы давления на
боковую поверхность рассчитывают усилие раздвижения полуформ при вертикальной
плоскости разъема и соответственно усилие запирания таких форм.
, т.е.
половина величины металлостатического напора. По величине силы давления на
боковую поверхность рассчитывают усилие раздвижения полуформ при вертикальной
плоскости разъема и соответственно усилие запирания таких форм.
Большая роль в литейных технологиях отводится применению закону Архимеда – поведению твердых тел погруженных в жидкость, в нашем случае в расплав металла. Сила давления расплава на погруженное в него твердое тело рассчитывается:
![]() , где W – объемное водоизмещение, т.е.
объем расплава, вытесненного погруженным твердым (или жидким нерастворимым в
металле) теле. Если
, где W – объемное водоизмещение, т.е.
объем расплава, вытесненного погруженным твердым (или жидким нерастворимым в
металле) теле. Если ![]() , то имеет место равновесие, М
– масса погруженного в расплав тела (литейный стержень, частицы шлака, инородный
металл).
, то имеет место равновесие, М
– масса погруженного в расплав тела (литейный стержень, частицы шлака, инородный
металл).
При условии ![]() происходит погружение
(опускание) в расплав, а при
происходит погружение
(опускание) в расплав, а при ![]() – всплывание (подъем)
инородного тела. Итак, если масса литейного стержня меньше величины
"водоизмещения" – rW, то будет происходить всплывание стержня, и необходимо
применять дополнительные технологические приемы, чтобы предупредить это явление
(устройство жеребеек, увеличение размеров знаков стержней, приклеивание знаков
стержней к форме). Заметим, что в соответствии с законом Архимеда подъемная
сила на стержни и другие тела, погруженные в расплав легких сплавов меньше, чем
для тяжелых металлов пропорционально величине плотности расплава r.
– всплывание (подъем)
инородного тела. Итак, если масса литейного стержня меньше величины
"водоизмещения" – rW, то будет происходить всплывание стержня, и необходимо
применять дополнительные технологические приемы, чтобы предупредить это явление
(устройство жеребеек, увеличение размеров знаков стержней, приклеивание знаков
стержней к форме). Заметим, что в соответствии с законом Архимеда подъемная
сила на стержни и другие тела, погруженные в расплав легких сплавов меньше, чем
для тяжелых металлов пропорционально величине плотности расплава r.
Для однородной массы шлаковых частиц (флюсы, оксиды) без внутренних
пустот и раковин закон Архимеда преобразуется в виде соотношения плотностей
металла и шлака. В большинстве своем ![]() – для чугунов и сталей
– для чугунов и сталей
![]() г/см3, а
г/см3, а ![]() г/см3 и потому шлак всплывает
на поверхность в печах и ковшах. Это явление используют при разработке
процессов плавки, рафинирования металлов и сплавов. Для шлаковых частиц не
очень мелких размеров (более одного миллиметра) скорость всплывания рассчитывают:
г/см3 и потому шлак всплывает
на поверхность в печах и ковшах. Это явление используют при разработке
процессов плавки, рафинирования металлов и сплавов. Для шлаковых частиц не
очень мелких размеров (более одного миллиметра) скорость всплывания рассчитывают:
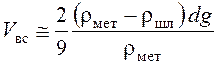 , где d – диаметр шлаковой частицы; g – ускорение силы тяжести.
, где d – диаметр шлаковой частицы; g – ускорение силы тяжести.
Для легких сплавов на основе магния и алюминия соотношение плотностей
оксидов и расплава металла иное, а именно ![]() (
(![]() г/см3,
г/см3, ![]() г/см3),
поэтому частицы оксидов тонут и располагаются в нижней части металлической
ванны.
г/см3),
поэтому частицы оксидов тонут и располагаются в нижней части металлической
ванны.
Для легких сплавов подбор состава покровных шлаков, обеспечивающих
их постоянное и стабильное расположение на поверхности расплава (![]() ), рассматривается в виде основного
технологического параметра.
), рассматривается в виде основного
технологического параметра.
На основе законов гидростатики рассчитываются усилия нагружения песчаных форм и запирания металлических форм. Для форм с горизонтальной плоскостью (поверхностью) разъема усилие на верхнюю полуформу, развиваемое металлостатическим давлением металла, определяется:
![]() , где hp – расчетный металлостатический напор; F
– проекция профиля полости на верхнюю горизонтальную плоскость формы. Если в
форме имеется стержень (или несколько стержней), то к величине Ррас
плюсуется подъемная сила стержня:
, где hp – расчетный металлостатический напор; F
– проекция профиля полости на верхнюю горизонтальную плоскость формы. Если в
форме имеется стержень (или несколько стержней), то к величине Ррас
плюсуется подъемная сила стержня:
![]() .
.
Естественно при ![]() подъемная сила стержня
отсутствует.
подъемная сила стержня
отсутствует.
Отсюда, усилие нагружения (закрепления) форм при горизонтальной плоскости разъема равно:
![]() , где Мвер – масса верхней полуформы.
, где Мвер – масса верхней полуформы.
Усилие запирания металлических форм с вертикальной плоскостью разъема при свободной (гравитационной) заливке рассчитывают по усилию, действующему на боковую поверхность:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.