Гидромеханические явления процесса формирования отливок, страница 4

, где Н – высота металлостатического напора; m – коэффициент расхода, 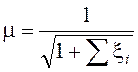, где  - сумма коэффициентов местных сопротивлений при сужении, расширении, повороте потока, в местах установки фильтров и др. Величина каждого коэффициента принимается на основе справочных данных.

Для запертой (заполненной) литниковой системы скорости потоков в других элементах рассчитывают на основе применения уравнения неразрывности течения. Наиболее распространенное представление уравнения неразрывности имеет вид:

, где r – плотность расплава; t – время;  – дивергенция вектора скорости, 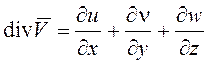, u, n, w – проекции вектора скорости объемного расширения расплава по координатам x, y, z.

Течение металла по литниковым каналам можно рассматривать одномерным, а значит для этого случая .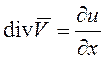

В преобладающем большинстве технологических процессов литья плотность металла в процессе течения можно считать постоянной, т.е. 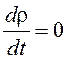 и тогда 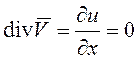, u = const.

Другими словами при постоянном поперечном сечении скорость потока на всем протяжении неизменна. А при изменяющемся поперечном сечении постоянным сохраняется расход расплава и это условие записывается: , т.е. , где F_ст и v_ст – площадь сечения стояка и скорость потока в нем; F_шл и v_шл – площадь сечения шлакоуловителя и скорость потока в нем; F_пит и v_пит – площадь сечения питателя и скорость потока в нем.

Из записанного выше выражения определяются скорости во всех других сечениях, если известна скорость потока в одном из сечений. Например, скорость потока в шлакоуловителе рассчитывается:

.

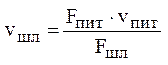Однако в некоторых частных случаях, например, в литье под давлением при очень малом сечении питателя r ¹ const, поскольку при входе в полость литейной формы происходит распад струи расплава и дальнейшее заполнение осуществляется металловоздушной смесью, плотность которой примерно на порядок меньше плотности компактного металла. В этом случае при расчете скорости следует руководствоваться уравнением неразрывности в общем виде:

 или .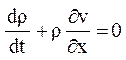

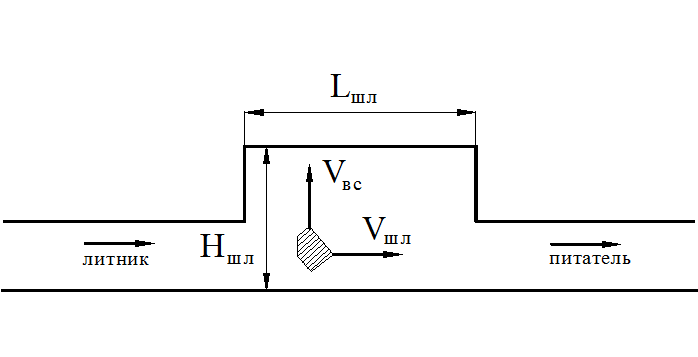
Рис. 29. Схема задержания инородных частиц в шлакоуловителе (к расчету шлакоуловителя)

Из элементов литниковой системы специальное предназначение отводится шлакоуловителю – для задержания шлаковых, песчаных и других инородных частиц, плотность которых меньше плотности расплава. Задержание инородных частиц в шлакоуловителе происходит за счет всплывания их в верхнюю часть шлакоуловителя, что делает невозможным попадание их в питатель, а затем и в полость литейной формы (рис. 29). Геометрические параметры шлакоуловителя, а именно длина его l_шл рассчитывается из условия всплывания частицы до верхней части шлакоуловителя в процессе течения расплава по этой части литниковой системы. Запишем условие равенства времени движения частицы в потоке расплава по длине шлакоуловителя и времени всплывания частицы от низа до верха шлакоуловителя: . Время движения по длине шлакоуловителя представим: , а скорость v_шл потока металла по шлакоуловителю определим из уравнения неразрывности:

.

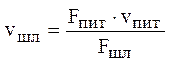Время всплывания частиц до верха шлакоуловителя 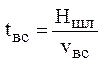. Скорость всплывания частицы v_вс в зависимости от режима движения определится по одной из двух формул. Для ламинарного потока по формуле Стокса:

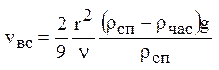, а для турбулентного:

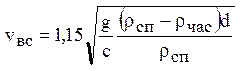, здесь d – диаметр частицы, d = 2r; r_сп – плотность сплава; r_час – плотность частицы; n – коэффициент кинематической вязкости сплава; с – эмпирический коэффициент.

Запишем равенство времени всплывания и длительности движения частицы по длине шлакоуловителя:

.

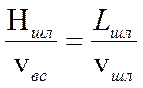И отсюда длина шлакоуловителя выразится:

.

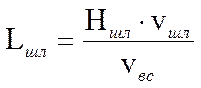2.2.3. Анализ особенностей течения металла в литниковых системах

различных типов и методика расчета минимального сечения