Дифференциал функции. Геометрический смысл дифференциала. Использование полного дифференциала для нахождения ошибок

Для независимой переменной дифференциал равен приращению dx=Δx.

Тогда дифференциал функции  dy=bdx, где b - есть предел, т.е. по смыслу производная, тогда

dy=y'dx  отсюда y'=dy/dx

          3.3. Свойства дифференциала

1) d(cu)=cdu 

2) d(u+v)=du+dv

3) d(uv)=vdu+udv 

4)   

3.4. Геометрический смысл дифференциала

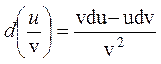
Дифференциал функции есть приращение ординаты касательной, проведенной к графику этой функции в  точке х₀.

 

Рис. 3.1

Применение дифференциала для приближенных вычислений

Приращение функции примерно равно дифференциалу Δy≈dy. Дифференциал по определению равен:  dy=y'dx.

Тогда мы можем выразить функцию следующим образом

Δy=f(x₀+Δx)-f(x₀)  

f(x₀+Δx)-f(x₀)=y'dx

f(x₀+Δx)=f(x₀)+y'dx

Например,

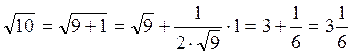
3.5. Функция  нескольких переменных

Функция нескольких переменных: площадь s=s(x,y), объем v=v(x,y,z), уравнение состояния идеального газа PV=RT т.е. p=p(v,T)  и  тому подобное.

Определение: Переменная z называется функцией двух аргументов x и y, если некоторым парам значений (x, y) по какому-либо правилу или закону ставится в соответствие определенное значение z:  z=f(x,y)

Частные производные первого порядка

Частной производной первого порядка функции z=f(x, y) по аргументу  х в  рассматриваемой  точке (x, y) называется предел

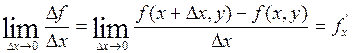
Обозначение:

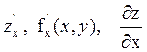
          Частный и полный дифференциал функции двух аргументов

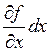Пусть функция z=f(x,y) имеет две частные производные  и . Произведение  называется частным дифференциалом функции f(x,y) по х и обозначают 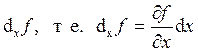. Аналогично   .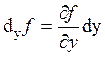

Сумму частных дифференциалов функции z=f(x,y) называют ее полным дифференциалом и обозначают .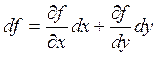

Обобщая на функцию многих переменных полный дифференциал можно определить как сумму частных дифференциалов

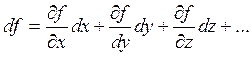
3.6. Использование полного дифференциала для нахождения ошибок

Пусть скорость определяют по формуле v=s/t, тогда ошибка измерения скорости может быть определена с помощью полного дифференциала:

    или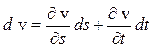    

Тогд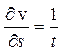а        ,   а 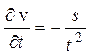    ,  для полного дифференциала получаем:

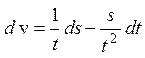,  заменим дифференциал d на ошибку Δ, а вместо знаков минус ставим знаки плюс, т.к. ошибки всегда складывают.

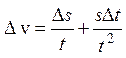   - это абсолютная ошибка.

Для относительной ошибки .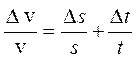

3.7. Использование производной и дифференциала для построения графиков функций

Рассмотрим несколько теорем без доказательств.

Теорема 1. (Формула Лагранжа)

Если функция f(x) имеет производную на (a,b),  и

, то можно указать такую точку с, a < c < b, что

.

Теорема 2. (достаточный признак монотонности)

1)  Если  на (a; b), то f монотонно возрастает на  (a; b);

2)  Если  на (a; b), то f монотонно убывает на  (a; b);

Теорема 3. (признак постоянства функции)

Для того, чтобы функция была постоянной на (a; b), необходимо и достаточно, чтобы  на (a; b)

Если первая производная на интервале больше нуля, то функция на этом интервале возрастает. Если первая производная  на интервале меньше нуля, то функция на этом интервале убывает. Если первая производная на интервале равна нулю, то функция на интервале не изменяется.

Теорема 4. (необходимый признак экстремума)

Если в точке экстремума существует производная, то она равна нулю .

Теорема 5. (достаточный признак экстремума)

Пусть функция f(x) непрерывна в точке x₀,

1)  если  на (a; x₀) и  на (x₀; b), то в точке x₀  функция f(x) имеет минимум;

2)  если  на (a; x₀) и   на (x₀; b), то в точке x₀  функция f(x) имеет максимум;

Таким образом, с помощью первой производной можно определить экстремумы функции. Необходимо найти первую производную и приравнять ее к нулю, решив полученное уравнение, определим точки экстремума.  Если первая производная при переходе через точку экстремума меняет знак с (+) на (-), то в этой точке она имеет максимум. Если первая производная при переходе через точку экстремума меняет знак с (-) на (+), то в этой точке она имеет минимум.