15.1. Регрессионный анализ
Вычисление коэффициента корреляции позволяет установить тесноту и направление связи между признаками. Однако это не позволяет установить, насколько в среднем изменится варьирующий признак при изменении на единицу измерения другого, связанного с ним признака. Решение этого вопроса возможно с помощью регрессионного анализа.
Функция, позволяющая по
величине одного признака (х) находить средние (ожидаемые) значения другого
признака 
, связанного с х корреляционно, называется
регрессией.
В отличие от коэффициента корреляции, показатели регрессии являются величинами именованными.
Уравнения регрессии, описывающие зависимости между случайными величинами, могут быть различными, в данной работе будет рассмотрена лишь линейная регрессия, которая выражается простым уравнением линейной зависимости:
Рассмотрим только случай линейных уравнений регрессии, то есть когда параметры связаны соотношением:
Задача регрессионного анализа – найти числа k и c0. После этого можно подставлять любые значения Х и
прогнозировать соответствующие ему средние значения .
Уравнений регрессии два. В первом Х является независимой
переменной, а – зависимой, и оно носит название «Y на Х». У другого наоборот, независимая переменная Y, а зависимая 
и
оно называется уравнением «Х на Y».
Рассмотрим связь двух случайных величин: Х – рост, Y – вес. Поскольку речь будет идти о выборке, поэтому будем
оперировать выборочными параметрами.
Основным моментом в регрессионном анализе является поиск «наилучшей» линии, проходящей через экспериментальные точки на графике взаимоотношений между показателями Х и У.
Для определения «наилучшей» линии обычно используют метод наименьших квадратов, который позволяет выбрать линию, сумма расстояний от которого до каждой точки будет наименьшей. Но поскольку этот метод достаточно сложный, мы используем более доступный подход в объяснении нахождения такой линии.
Обратимся к рис. 15.1а. Пусть мы имеем две выборки, взятые из одного корреляционного облака. Допустим, в первой выборке из 20 человек значения роста х1 -лежат в области малых значений, например, все 20 человек имеют рост 165 см. Пусть во второй выборке из 20 человек рост х2 лежит в области больших значений, например, все 20 человек имеют рост 180 см. Вес у этих людей может оказаться разным, поэтому каждой выборке будет соответствовать целая группа значений веса – точки на соответствующих вертикалях. Эти точки на линии распределены с разной плотностью: плотность уменьшается к краям. Это отображено соответствующими графиками-колоколами (нормального распределения). Центры же колоколов являются средними арифметическими `Y1 и `Y2 , соответствующими х1 и х2. Через эти точки проводится прямая, которая являться графиком уравнения регрессии. Из математики мы знаем, что любую линию на графике можно описать с помощью какого-либо уравнения: y=x2, y=sin(x), y=kx и т.д. (см. рис. 14.1).
В данном случае получившаяся прямая также описывается уравнением линейной зависимости и носит название « Y на Х »
, где коэффициент
пропорциональности вычисляется по формуле: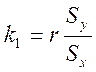 
.
В данном уравнении все параметры кроме x и имеют
конкретные численные значения. Поэтому, подставив эти числа, перемножив и
собрав свободные члены вместе, мы получаем уравнение прямой, имеющее более
привычную для нас форму:
.
Пользуясь этим уравнением можно найти ,
подставив известное значение x.
На графике для другого уравнения «X на Y» алгоритм остается тем же (рис. 15.1б ): отбираются две выборки с определенным весом y1 и y2 ® строятся колокола распределения значений роста, соответствующих этим двум весам ® определяются `Х1 и `Х2 ® через них проводится прямая линия графика второго уравнения регрессии « Х на Y »:
, коэффициент пропорциональности k2 вычисляется по формуле:
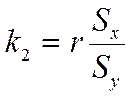, после подстановки перегруппировки получим уравнение вида:
.
Пользуясь этим уравнением можно найти 
,
подставив известное значение y.
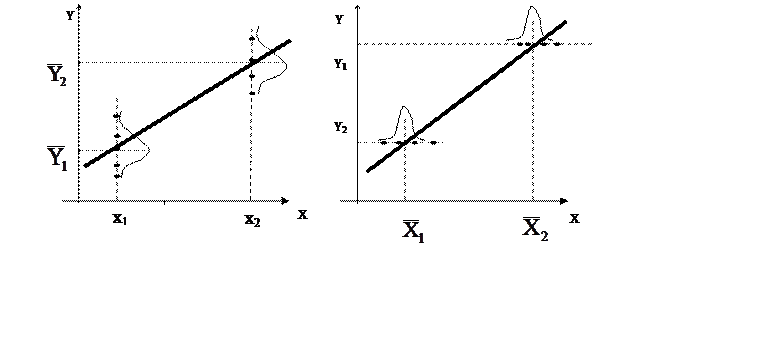
а б
Рис. 15.1 Принцип построения уравнений регрессии: а – при усреднении Y; б – при усреднении Х.
Термин был введен Френсисом Гальтоном, который исследовал закономерности СВ в области биологии и является одним из основоположников биометрии, науки, которая бурно развивается в наши дни. Гальтон проводил исследование связи роста детей и роста родителей.
Связь между этими случайными величинами, очевидно, существует, и достаточно сильная. Гальтон ожидал получить величину коэффициента корреляции около 0.7. Однако на достаточно большой выборке Гальтон получил значение r между 0.5 и 0.6. Это оказалось неожиданно мало. Гальтон, исходя из того, что такая величина коэффициента корреляции имеет какую-то биологическую целесообразность, выдвинул следующую идею. Он предположил, что при большой величине коэффициента корреляции корреляционное облако неизбежно разделилось бы на два. То есть у высоких родителей рождались бы с большей вероятностью высокие дети, а у низких – низкие. И постепенно единая популяция разделилась бы на "великанов" и "лилипутов". Таким образом, не очень высокий уровень коэффициента корреляции свидетельствует о наличии тенденции возврата (регресса!) к центру облака для сохранения единого сообщества. Значит, у слишком высоких или слишком низких людей рост детей будет возвращаться к среднему росту.
Эта идея имеет смысл, выходящий далеко за рамки статистической задачи о связи роста детей и роста родителей. За этим просматривается роль разброса и отсутствия предопределенности, как факторов устойчивости биологических видов. Конечно, хотелось бы в области медицины иметь иногда жесткие связи: пропил неделю аспирин и на 100% избавился от простуды, но жесткость связей в живой природе опасна: ведь тогда получается, что чем жестче зависимости, тем реальнее опасность появления такого "вируса", который всех "функционально", т.е. стопроцентно уничтожит.
Вывод: именно для выживания в любых ситуациях нужны разброс, изменчивость и подвижность связей между любыми параметрами. То есть разброс и отсутствие жестких связей являются необходимыми условиями сохранения видов и их развития.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
