14.1. Корреляционный анализ
Корреляционный и регрессионный анализ – два способа выявления связи между случайными величинами
В медико-биологических исследования большое внимание уделяется установлению связей между различными параметрами, признаками или явлениями.
В математике для выражения зависимости между переменными величинами
используется понятие функции. О функциональной зависимости говорят в том
случае, когда определённому значению одной переменной соотносится только одно
значение другой переменной. В общем виде эта зависимость записывается так: y=f(x). Так
например, длина окружности однозначно и линейно связана с радиусом
окружности: L=2
R.
При: R = 1, L = 2, а
при R = 2, L = 4 и
т.д. Линейную зависимость в математике принято выражать в следующем виде: y=kx +b. Где k – угол наклона прямой к оси x
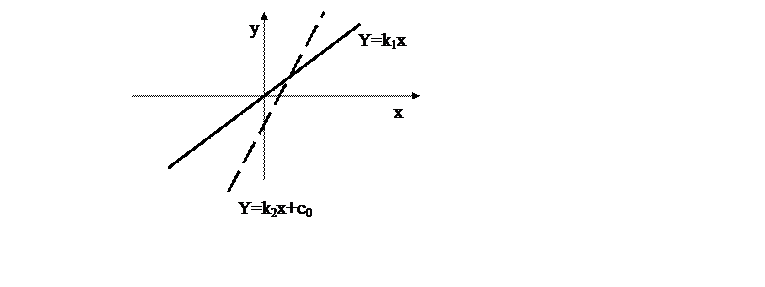
Рис. 14.1
Известные формулы физики также указывают на наличие функциональной зависимости
между различными физическими величинами. Например, закон Ом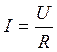а 
устанавливает связь между силой тока,
напряжением и сопротивлением проводника.
Однако в медико-биологических экспериментах функциональные зависимости встречаются далеко не всегда, а чаще одному значению признака соответствует несколько значений другого признака. Например, при одном и том же росте, вес различных людей может быть различен, но между средними значениями этих показателей имеется определённая зависимость.
Закономерности при работе со случайными величинами могут иметь только статистический, а это значит – усредненный, характер. По отношению же к конкретному объекту наблюдения эти закономерности могут иметь только приблизительный и вероятностный характер.
Такого рода зависимость между переменными случайными величинами X и Y, при которой каждому значению одной из них соответствует не какое-то конкретное значение, а определённая групповая средняя другой величины, называется стохастической (что в переводе на русский означает - вероятностной), а если она линейная, то связь называют корреляционной или просто корреляцией.
Примеров корреляции можно привести достаточно много. В медицине это количество простудных заболеваний за месяц на участке и средняя температура месяца, в - социологии - количество браков в году и число новорожденных в следующем году, в сельском хозяйстве - количество выпавших осадков и урожайность на полях, в педагогике – количество прочитанного материала перед экзаменом и оценка на экзамене и т.д.
Раздел математической статистики, занимающийся установлением взаимосвязей между случайными величинами называется корреляционно-регрессионным анализом.
С помощью корреляционного анализа определяется теснота или сила связи между случайными величинами, а также направление связи между ними. Сила связи при этом характеризуется одним числом – коэффициентом корреляции. Величина коэффициента корреляции может быть в пределах от 0 до ±1. Ноль означает, что связи совсем нет, а единица получается при другой крайности – когда связь оказывается абсолютной, то есть функциональной, 100-процентной. Тогда число 0.8 в каком-то случае означает, что сила связи между случайными величинами в этом случае составляет 80% от абсолютной, функциональной.
При этом, если с увеличением одной величины возрастает и другая, то корреляционная связь называется прямой. Коэффициент корреляции в данном случае положительный. Если с ростом одной величина другая, связанная с ней величина уменьшается, связь называется обратной, а коэффициент корреляции будет отрицательным.
Регрессионный анализ позволяет описать форму зависимости между СВ с помощью уравнений регрессии (линейных, квадратичных, показательных и т.д.) . Кроме того, с помощью уравнений регрессии можно зная одну величину предсказать другую. Установление взаимосвязи между различными признаками и показателями функционирования организма позволяет по изменениям одних из них судить о состоянии других. Очевидно, каждый из вас занимался регрессионным анализом, если пытался определить свой вес Y, зная свой рост X, с помощью математического уравнения: Y = X – 100.
Регрессионный и корреляционный анализ тесно связаны друг с другом.
Прежде чем приступить к описанию коэффициента корреляции попробуем рассмотреть вспомогательную величину – коэффициент ковариации.
Именно из этого коэффициента можно получить коэффициент корреляции.
Слово "ковариация" в переводе означает "соизменение". Наличие связи между случайными величинами выражается в том, что параметры X и Y в значительной степени изменяются согласованно. Совместное изменение СВ принято называть соизменение. В случае роста и веса очевидно, что у высокого человека, вес окажется скорее всего большим, а если рост ниже среднего, то и вес окажется ниже среднего веса.
Для характеристики степени соизменения в математической статистике вводится коэффициент ковариации. а) Коэффициент ковариации в генеральной совокупности.
Он обозначается буквой m и определяется по формуле:
.
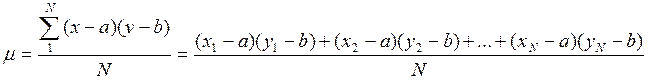Здесь: а – математическое ожидание случайной величины Х;
b – математическое ожидание случайной величины Y;
N – объем генеральной совокупности.
По смыслу параметр m является средним произведением отклонений обеих случайных величин от своих средних в генеральной совокупности. Иначе говоря, у него смысл среднего соизменения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
