Корреляция. Корреляционный анализ. Коэффициент корреляции. Проверка значимости коэффициента корреляции, страница 3

                                                                              II                        I

 

III                         IV

	X

 

а)                                                                      б)               

 

в)                                                                     г)

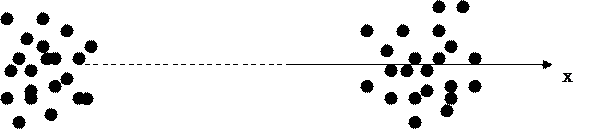
Рис. 14.2  Корреляционное облако в разных случаях: а и б – при отсутствии связи;  в – при прямой связи; г – при обратной связи.

Подытожим: чем более вытянуто корреляционное облако, тем больше сумма в числителе формулы и тем сильнее связь между случайными величинами. Поэтому построение корреляционного облака является очень наглядным и эффективным способом оценки наличия связи между изучаемыми случайными величинами.  б) Выборочный коэффициент ковариации.

Для оценки истинного значения коэффициента ковариации служит выборочный коэффициент  ковариации m_xy:

.  

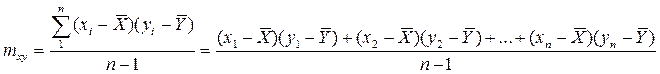В заключение укажем на  недостаток коэффициента ковариации. Он  хорош для случая отсутствия связи между случайными величинами. Если  он равен нулю, то  связи точно нет. Его недостаток проявляется при наличии связи. Этот недостаток  заключается в том, что коэффициент ковариации имеет размерность, соответствующую произведению размерностей обеих случайных величин. Следовательно, величина коэффициента ковариации зависит от масштаба измерения.  Если рост измерять в метрах, сантиметрах, и т.д., а вес в  килограммах, граммах миллиграммах и т.д,  то будут получаться разные численные значения m (или m_xy). Следовательно по абсолютной величине числа m или m_xy  сказать что-либо о силе связи невозможно.

Для устранения  недостатка коэффициента ковариации из него был выведен другой коэффициент, характеризующий связь между случайными величинами, - коэффициент корреляции

14.3.  Коэффициент корреляции

а) Коэффициент корреляции в генеральной совокупности.

Он обозначается буквой r и получается из m  с помощью нормировки. Формула для перехода от m к r имеет вид:

.                                                

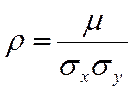Важно отметить  то, что таким образом  устраняется размерность, и коэффициент, характеризующий силу связи, становится относительным и изменяется в пределах от 0 до ±1. Коэффициент корреляции равен нулю при отсутствии связи между случайными величинами. Максимальное значение, равное единице,  он принимает когда корреляционная связь переходит в функциональную, то есть становится абсолютной на 100%.

Выделяют три диапазона значений коэффициента корреляции:

·  0 – 0,3 – слабая корреляция (то есть до 30% от функциональной);

·  0,3 – 0,7 – средняя корреляция;

·  0,7 – 1,0 – сильная корреляция (свыше 70% от функциональной).

Если в формулу  подставить  формулы для m, s_x и s_y, то получится расчетная формула для r: 

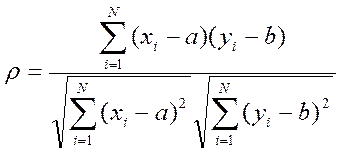.                                      б) Выборочный коэффициент корреляции.

Оценивают истинное значение коэффициента корреляции с помощью выборочного коэффициента корреляции, обозначив его как r. 

При переходе  от генеральной совокупности к выборке осуществим необходимые замены.

r   ®   r

m   ®   m_xy

s_x ®   S_x

s_y  ®   S_y

a  ®  

b  ® `

Сделав необходимые замены в формулах получим формулу  для выборочного коэффициента корреляции:

.                                                   

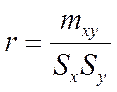Расчетная формула принимает вид: