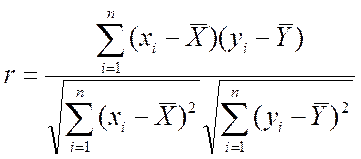Корреляция. Корреляционный анализ. Коэффициент корреляции. Проверка значимости коэффициента корреляции, страница 4

.                               

Из последней формулы видно, что определение коэффициента корреляции требует достаточно большой вычислительной работы. Должны быть вычислены средние арифметические значения для обеих случайных величин, потом отклонения каждого значения от средних, их квадраты для сумм в знаменателе, и произведения для суммы в числителе. Даже при небольшой выборке в 10-20 объектов это трудоемкая задача, при этом легко допустить техническую ошибку. Для облегчения  вычислений обычно заполняется специальная таблица, форма которой приведена в таблице.

Таблица для расчета коэффициента корреляции

14.4. Проверка значимости коэффициента корреляции

Поскольку значение r в выборке может отличаться от r в генеральной совокупности, необходима проверка значимости коэффициента  корреляции. Кроме этого, уменьшение выборки всегда понижает достоверность, значимость получаемых чисел. Кроме того,  в случае определения коэффициента корреляции. Малая выборка делает значение r более подверженным случайности. Выборка из 3-5  человек может не только дать не очень соответствующее действительности численное значение r. Но и даже исказить информацию о связи СВ.  Если среди этих 3-х окажутся: один с ростом и весом около средних, другой имеет рост  выше среднего роста, а вес ниже среднего веса,  а третий  рост  ниже, а вес  выше среднего, то коэффициент корреляции получиться вообще отрицательным, поскольку  соизменение – обратное.  И можно делать вывод, что между ростом и весом обратная связь: чем выше человек, тем  он легче!

Поэтому всегда вместе с вычислением самого значения r еще "проверяют его значимость".

Поэтому всегда вместе с вычислением самого значения r еще "проверяют его значимость". Для этого необходимо определить его стандартную ошибку. При достаточно большом числе наблюдений (n ≥ 100) стандартная  ошибка  коэффициента корреляции определяется по формуле:

.

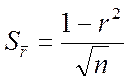Если число наблюдений меньше 100, то рекомендуется  пользоваться другой формулой:

.

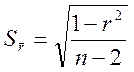Имея значения коэффициента корреляции и его ошибки, можно проверить предположение о равенстве коэффициента корреляции нулю, т.е. установить отсутствие связи между исследуемыми параметрами. Для проверки этой гипотезы используется критерий t-Стьюдента. При этом выдвигается две гипотезы:

·  Н₀ – связь между параметрами отсутствует;

·  Н₁ - связь между параметрами имеется.

Для проверки гипотез вычисляется соотношение между найденным значением коэффициента корреляции и его стандартной ошибкой, т.е. находится критерий t:

.

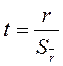После деления  для малых выборок получается формула:

.

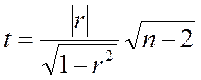Нулевая гипотеза отвергается, если t ≥ t_табл для k = n – 2 и заданного уровня значимости α (или вероятности Р=1-α). При t < t_табл нулевая гипотеза принимается и отклонение выборочного коэффициента корреляции от нуля считается чисто случайным.

Например, при  t = 2.52 и n = 14 нулевая гипотеза отвергается с уровнем значимости  α= 0.05, т.к.  t_табл  = 2.18, однако не для уровня α = 0.01 (t_табл = 3.05). Это означает, что мы не можем гарантировать выполнения гипотезы в 99 случаях из 100, а лишь в 95%.