Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными. Замена переменных на примере однородного уравнения

§6.   Дифференциальные уравнения

6.1. Общие сведения о дифференциальных уравнениях

Дифференциальным уравнением называется уравнение содержащее не только функцию f(x) , но и ее производные  или дифференциалы.

В общем виде дифференциальное уравнение можно записать:

F(x, f(x), )=0   или   F(x, y,)=0

Если искомая функция y=f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным. Если функция U=f(x,y,z,...,t) зависит от двух и большего числа аргументов, то уравнение будет содержать частные производные. Такое уравнение носит название дифференциального уравнения в частных производных.

Порядком дифференциального уравнения называется порядок наивысшей производной или дифференциала входящих в уравнение.

Например:   – уравнение 1-го порядка.

    – уравнение 2-го порядка и т.д.

Дифференциальные уравнения широко используются при изучении явлений и процессов во многих областях науки.

Общим решением дифференциального уравнения порядка k называется функция y=f(x, C₁, C₂, ..., C_k) от х с произвольными постоянными C₁, C₂, ..., C_k , обращающая  это уравнение в тождество.

Частное решение: частные решения получаются в случае, если постоянные равны конкретному выражению. На практике частное решение получают из общего с учетом тех условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий: ,           и т.д.

Например:  , решением будет уравнение вида

Например: установить закон изменения скорости свободно падающего тела

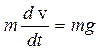
,  при   и тогда    

6.2. Дифференциальные уравнения с разделяющимися переменными

Уравнение вида:   

называется уравнением с разделяющимися переменными.

Поделив на  получим 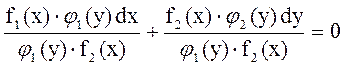, при условии что , тогда получаем: .

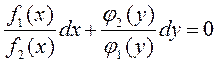Это уравнение называется уравнение с разделенными переменными.

Проинтегрируем:

.

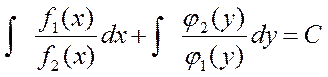Это общее решение уравнения с разделенными переменными, для получения частного решения надо определить С из начальных условий.

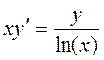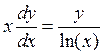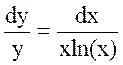Пример 1: Решить уравнение  при x=e,  y=1, ,     разделим левую и правую части уравнения на произведение , тогда получим: .    Найдем решение

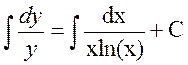, получаем   ,  , из начальных условий определим С:   тогда  и частное решение: .

Пример 2: Решить уравнение , ,    ,  ,   , .

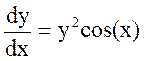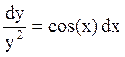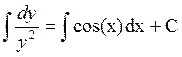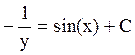6.3. Замена переменных на примере однородного уравнения  

Уравнение вида 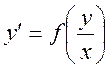 называется  однородным дифференциальным уравнением.

Сложность применения метода разделения переменных связана со сложностью вычисления интегралов. Вообще говоря, способы взятия интегралов во многом напоминают способы решения дифференциальных уравнений. Так замена переменных или самих функций часто упрощает решение дифференциальных уравнений. В частности для однородного уравнения получаем: 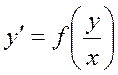 , замена   ,   ,   , здесь использовали правило нахождения производной произведения или  . В последнем уравнении переменные уже разделяются:

, , ,  .

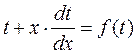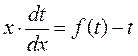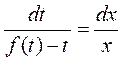6.4. Линейные дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка, содержащие первую степень функции и ее производных называется линейным. Подобные уравнения могут быть неоднородными или с правой частью зависящей от времени и однородными – с правой частью равной нулю. В общем случае неоднородное линейное дифференциальное уравнение второго порядка записывают в виде:

, где f₁(t), f₂(t), f(t) – функции, в общем случае зависящие от времени.

Если f(t) = 0, то уравнение называется однородным. В простейшем случае, когда коэффициенты f₁ и f₂  не зависят от времени, уравнение решается с помощью подстановки экспоненциальной зависимости с неизвестным показателем экспоненты A×e^(rt), где предэкспоненциальный множитель А находится из начальных условий, а неизвестное r из квадратного уравнения, называемого характеристическим, получаемым после сокращения уравнения на экспоненту, входящую в каждое слагаемое:

Решение этого уравнения имеет два корня: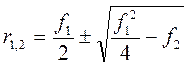

По известным корням можно составить общее решение однородного уравнения, записываемое следующим образом:  .  Неизвестные константы интегрирования С₁, С₂ находятся из двух начальных условий, например, из задания в начальный момент времени значения функции и ее производной. После нахождения констант интегрирования и подстановки в общее решение получаем частное решение однородного уравнения.  Но если находится общее решение неоднородного уравнения с правой частью, то для его получения к общему решению однородного уравнения необходимо прибавить одно из частных решений неоднородного.

Например:        общее решение  , зададим начальные условия для получения частного решения: . Найдем первую производную:

, теперь подставим конкретные значения в уравнения и получим следующую систему:

отсюда получим  

и тогда частное решение равно:

6.5. Прикладные задачи физики

Зависимость числа нераспавшихся ядер атомов радиоактивного вещества от времени. Ядра атомов радиоактивных элементов с течением времени распадаются. Опытным путем установлено, что скорость распада пропорциональна числу не распавшихся в данный момент ядер атомов. В аналитической форме это можно записать так:

dN/dt= - N, где N - число не распавшихся в данный момент ядер атомов; t - время;  - постоянная распада. Минус означает, что с течением времени число нераспавшихся ядер атомов уменьшается и производная убывающей функции отрицательна. Скорость же по смыслу - положительная величина.

Установим зависимость числа нераспавшихся ядер атомов радиоактивного вещества от времени, если при t = 0 число нераспавшихся ядер атомов N = N₀. Разделим переменные в уравнении  и проинтегрируем левую часть по N, а правую по t:

.

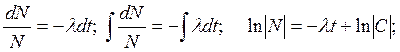
Полагая в последнем уравнении t = 0 и N = N₀, находим