Теорема 6. (достаточный признак выпуклости)
Если
на интервале (a; b), то функция f(x) выпукла вниз
на (a; b); если 
на (a; b), то функции f(x) выпукла вверх
на (a; b).
Также по второй производной в точке экстремума можно определить максимум в данной точке или минимум. Если вторая производная в точке экстремума меньше нуля, то в данной точке будет максимум, а если вторая производная в точке экстремума больше нуля, то в данной точке будет минимум. Приравняв вторую производную к нулю и, решив данное уравнение, находят точки перегиба функции.
3.8. Схема построения графика функции.
1. Найти область определения функции
2. Найти область значений функции
3. Исследовать функцию на четность и нечетность
4. Исследовать функцию на периодичность
5. Рассмотреть поведение функции в окрестностях точек разрыва
6. Определить поведение функции на бесконечности
7. Найти точки пересечения графика функции с осями
8. Найти точки экстремума и значения функции в этих точках
9. Определить точки перегиба и значения функции в этих точках
10. Определить интервалы выпуклости и вогнутости функции
11. Составить сводную таблицу и построить график.
Пример 1: построение
графика функции 
.
1. Область определения функции вся числовая ось.
2. Область значений – всюду большая нуля.
3.
Функция четная: 
.
4. Функция не периодичная.
5. Функция не имеет точек разрыва.
6.
На бесконечности функция стремится к нулю: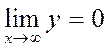 
.
7. x=0, y=1; y≠0;
8.
Находим первую производную 
; 
на ( - ∞; 0) – здесь функция монотонно возрастает,
на (0,+∞) – здесь функция монотонно
убывает, в точке х=0 
меняет знак с плюса на минус,
т.е. 0 – точка максимума и у(0)=1.
9.
Находим вторую производную: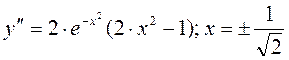 
- точки перегиба, там 
.
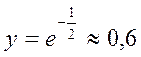10.
на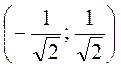 
здесь
функция выпукла вверх, 
на 
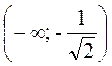и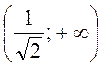 
- здесь функция выпукла вниз.
11. y(0)=1 – точка максимума.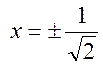 
- точки перегиба,
у=0,6.
Рис. 3. 2
Пример 2: построение графика функции y=x3-3x.
1. Функция определена для всех х.
2. Область значений – вся числовая ось.
3. Функция нечетная, т.к. f(-x)= - f(x). Выразим, (-x)3-3(-x)=-(x3-3x)
4. Функция не периодическая.
5. Функция не имеет точек разрыва.
6.
Поведение функции на бесконечности: 
и 
7. x=0, y=0; y=0, x3-3x=0, x(x2-3)=0, x=0, x1,2=±1,7
8.
Находим первую производную: 
; приравниваем к нулю: 
, находим корни данного уравнения: х1,2=±1.
9. В точке х=-1 находится максимум y(-1)=-1+3=2; В точке х=+1 находится минимум, т.к. y(1)= 1-3=-2.
10.
Точки перегиба определяем с помощью вторых производных. 
, 
на
интервале, следовательно кривая выпукла на интервале (-∞, 0) и, если, 
на интервале, следовательно кривая вогнута
на интервале (0, +∞).
11. Функция нечетная: f(-x)= - f(x). Y(-1)=2; y(-2)=-2;
Рис. 3. 3
Пример 3: Реакция организма на введенный лекарственный препарат может выражаться в понижении температуры, повышения давления и т. д. Степень реакции зависит от назначенной дозы лекарства. Пусть х обозначает дозу назначенного лекарственного препарата, а степень реакции у описывается функцией f(x)=x2(a-x), где а – положительная постоянная. При каком значении х реакция максимальна?
Решение: Найдем
производную функции и приравняем ее нулю: 
,
отсюда критические точки х1=0, х2=2а/3. Значение х1=0
указывает на то, что в организм лекарство не вводилось. Исследуем точку х2=2а/3:
и 
,
следовательно в точке х2 =2а/3 функция имеет максимум. Таким
образом, х2 =2а/3 – это доза, которая вызывает максимальную реакцию.
Пример 4: Использование полного дифференциала для нахождения ошибки эксперимента.
Определить погрешность
измерения в определении скорости ΔV: если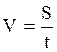 
, S=5·10-2 м, ΔS=0,2·10-2 м, t=3,5·10-6
с, Δt=0,05·10-6 с.
Скорость является функцией двух параметров V=V(S,t). Запишем полный дифференциал для этой функции:
.
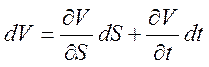Найдем частные производные 
и 
.
Напомним, что при нахождении частной производной по какому-либо параметру, другой параметр считается постоянной величиной.
Используя это правило получим:
, 
.
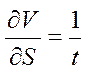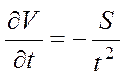Запишем полный дифференциал:
.
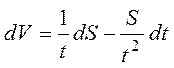Для определения ошибки заменим дифференциал d на ошибку Δ и все знаки плюс поменяем на минус, получим:
.
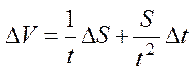В полученное уравнение подставим конкретные значения и определим ΔV. S=5·10-2 м, ΔS=0,2·10-2 м, t=3,5·10-6 с, Δt=0,05·10-6 с.
ΔV=1/3,5·10-6·0,2·10-2+0,2·10-2/(3,5·10-6)2·0,05·10-6=610 (м/с).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.