Первообразная функции. Неопределенный интеграл. Нахождение уравнения кривой по заданному тангенсу угла наклона касательной к оси Х

§4.  Первообразная функции. Неопределенный интеграл

4.1. Понятие первообразной функции

Во многих вопросах науки и техники приходится восстанавливать функцию по ее производной. Ранее мы предполагали, что по известному уравнению движения s=f(t)  мы путем дифференцирования  нашли сначала скорость v=ds/dt, а  затем  и ускорение  a=dv/dt. На деле, однако, довольно часто приходится решать обратную задачу: по закону изменения ускорения найти закон изменения скорости, т.е  восстановить ту функцию v=f(t), для которой а является производной, а затем, зная функцию v=f(t), найти ту функцию  s=f(t), для которой производной будет v.

Аналогично, зная массу m=f(x), непрерывно распределенную вдоль отрезка (0,х), дифференцированием можно найти линейную плотность =f(x). Но естественно возникает вопрос, как по заданному закону изменения плотности =f(x) найти величину распределенной массы, т.е. опять - таки, по известной функции =f(x) найти ту функцию m=f(x), для которой   является производной. Также и для силы, переменной на некотором промежутке dx. Зная величину силы, нужно найти величину работы как  A=f(F)

В математике все действия в основном группируются парами - прямое и обратное: сложение и вычитание (действие, обратное сложению), умножение и деление (действие, обратное умножению) и т. д. В предыдущей главе было введено еще одно действие - дифференцирование. Обратное дифференцированию действие называется интегрированием. Что такое действие дифференцирования? При помощи дифференцирования ищется производная от заданной функции. Следовательно, обратное действие - интегрирование - должно заключаться в следующем: задана производная, требуется найти функцию.

Действие обратное дифференцированию – интегрирование, т.е. нахождение функции F(x) по известной ее производной f(x)=    или дифференциалу   f(x)dx.

Определение: Функцию F(x) называют первообразной функции f(x), если для всех х из области определения функции выполняется равенство: =f(x)   или   dF(x)=f(x)dx.

Например,   F(x)=x³ является первообразной для f(x)=3x²  т.к. при любых х выполняется:

   или     d(x³)=3x²dx.

В общем случае если f(x) имеет первообразную функцию F(x), то совокупность F(x)+C также будет первообразной для f(x):

Определение: Совокупность первообразных F(x)+C  для данной функции f(x) или данного дифференциала f(x)dx называют неопределенным интегралом от функции f(x) и обозначают 

f(x)dx – подынтегральное выражение;

f(x) – подынтегральная функция;

С – постоянная интегрирования, ее обычно определяют из начальных условий.

4.2. Свойства неопределенного интеграла

1.  Производная от неопределенного интеграла равна подынтегральной функции:

2.  Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3.  Интеграл от дифференциала первообразной равен самой первообразной и постоянной:

4.  Постоянный множитель можно выносить за знак интеграла:

5.  Интеграл от суммы равен сумме интегралов:

4.3. Основные формулы интегрирования

                                       

                               

                                 

                 

                   

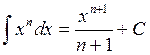
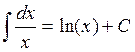
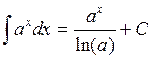
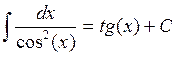
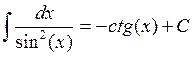
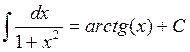
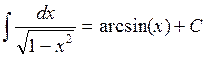
Непосредственное интегрирование

Способ основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличному виду. Пример: =

=

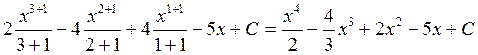
Интегрирование подстановкой (заменой переменных)

Способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.

,   ,   тогда   , 

Пример:

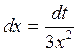,     , , тогда   =

= 

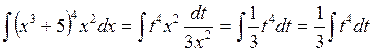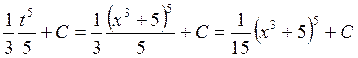
Интегрирование по частям

Если u=u(x) и v=v(x) дифференцируемые функции, то d(uv)=vdu+udv, откуда udv=d(uv) – vdu, интегрируя, получаем:

   или в окончательном виде формула для интегрирования по частям:

Пример:

,      ,       

,             

,   

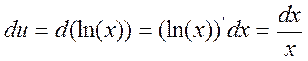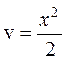
учитывая эти преобразования можно записать:

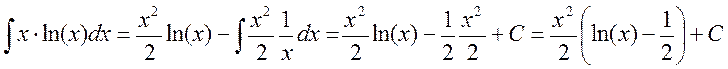
4.4. Нахождение уравнения кривой по заданному тангенсу угла наклона касательной к оси Х

Пусть тангенс угла наклона касательной к кривой относительно оси Х зависит от абсциссы точки касания: tgα=2x . Так как тангенс угла наклона касательной к оси Х равен производной, то

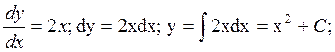
Это уравнение параболы, а с учетом постоянной С это целое семейство парабол. Графики некоторых парабол представлены на рисунке 4.1. Постоянная С в каждом конкретном случае определяется дополнительными условиями. Если указано, что кривая проходит через точку с координатами х=1, у=2, то подставив эти значения в уравнение 2=1²+С , получим уравнение одной определенной параболы: у=х²+1.

Рис. 4.1

4.5. Нахождение пройденного пути по заданной зависимости скорости от времени.

Пусть скорость материальной точки изменяется со временем по закону v=4t+2. Так как 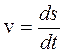, откуда . Интегрируя это равенство, получим  

.

Постоянная С находится из конкретных условий задачи. Например, задано дополнительное условие: в начальный момент (t=0) материальная точка находилась на расстоянии 25 м, тогда 25=0+0+С, т.е. С=25. В итоге имеем окончательное уравнение s=2t²+2t+25. Так как под скоростью можно понимать скорость не только механического движения, но и процесса (скорость усвоения препарата организмом, размножения бактерий, распада тканей, радиоактивного распада и т.д.), то путем интегрирования можно найти соответствующие зависимости от времени.