Информатика. Работа с 2D-графиками в MathCAD: Методические указания к компьютерному практикуму, страница 7

3) На графике протаскиванием мыши выделите рамкой фрагмент кривой, требующий увеличения. Точность выделения зоны увеличения можно контролировать с помощью специальных окон в диалоговом окне Min (Минимум) и Max (Максимум), в которых отражаются значения координат вершин прямоугольника выделения по обеим осям (рисунок 19).

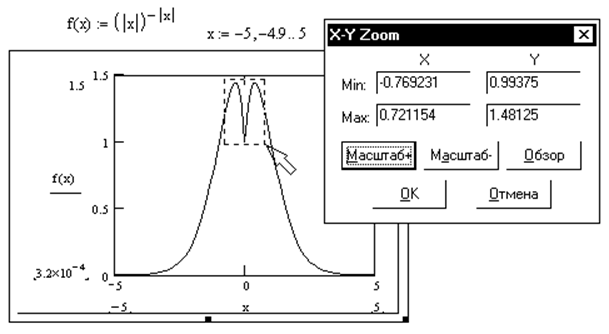
Рисунок 19 – Использование инструмента Zoom (Масштаб)

4) Когда область увеличения выделена, нажмите кнопку Zoom. Выделенный фрагмент займет всю область графика (рисунок 20).

Если какой-то шаг при последовательном увеличении фрагмента кривой был сделан неверно, то вернуться на предыдущий этап масштабирования можно при помощи кнопки UnZoom (Демасштабирование).

Используя кнопку FullView (Полный вид), можно вернуться к первоначальному виду графика.

5) После того как вы настроили изображение нужным образом, нажмите кнопку OK.

3.2 Трассировка графиков

Пожалуй, еще чаще, чем к инструменту масштабирования, приходится прибегать к использованию второго вспомогательного инструмента с панели Graph – Trace (Трассировка). При его помощи можно достаточно точно определить координаты интересующей точки (например, экстремума или корня уравнения).

Задание 6. Упрощенным способом постройте график функции . Найдите корни данного уравнения.

Порядок выполнения:

1) В соответствии с заданием постройте график функции, увеличьте размеры графической области и настройте линии сетки.

2) Используя инструмент масштабирования, увеличьте область графика, в которой четко будут видны точки пересечения линии графика с осью X (данные точки будут являться искомыми корнями уравнения).

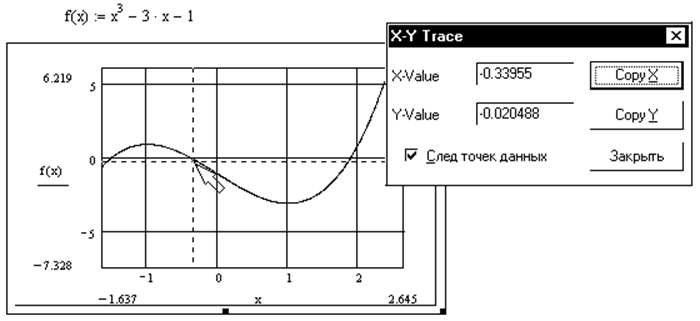
Рисунок 21 – Трассировка графика

3) Выделите построенный график и на панели Graph выберите инструмент  Trace (без выделения графической области данный инструмент будет недоступен).

4) В результате на графике появится своеобразный "прицел" в виде пересекающихся пунктирных прямых. Координаты прицела (точка пересечения прямых) отображаются в полях X- и Y- Value (координаты по X и Y) диалогового окна X-YTrace. Перемещать прицел можно, изменяя положение курсора (рисунок 21).

5) Когда нужная точка будет найдена (точка пересечения линии графика с осью абсцисс), нажмите кнопку CopyX (Копировать значение Х). При этом численное значение координаты по X будет скопировано в буфер обмена, откуда его можно будет вставлять в качестве значения переменных с помощью команды Insert (Вставка) меню Edit (Правка).

6) Ниже графика задайте переменную х1 и присвойте ей значение буфера обмена.

7) Аналогичным образом найдите и занесите в документ значение второго и третьего корня уравнения.

4 ГРАФИКИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ

Задание графиков в полярной системе координат с технической точки зрения не имеет никаких отличий от создания графиков на декартовой плоскости. Поэтому этот вопрос мы рассмотрим довольно кратко.

В полярной системе координат каждая узловая точка графика задается углом φ и радиус-вектором r(φ), имеющим длину равную значению заданной функции f(φ).  Узловые точки соединяются между собой линейными отрезками (рисунок 22). Поэтому, как и в декартовой системе координат, чем меньше заданный шаг изменения аргумента, тем плавнее получаются линии графика. График функции обычно строится при изменении угла φ в определенных пределах, чаще всего от 0 до 2π.

Для вызова шаблона полярного графика следует выбрать кнопку  на графической панели инструментов Graph или воспользоваться комбинацией клавиш [Ctrl]+[7]. Также вставить шаблон полярного графика можно с помощью пункта Polar Plot (Полярный график) подменю Graph меню Insert.

Как и в случае X-Y зависимости, для полярного графика существует два основных метода построения: быстрый способ и использование ранжированных переменных. Причем последний имеет большее значение ввиду того, что поменять стандартную величину изменения угла (от 0° до 360°) непосредственно на графической области нельзя.

В отличие от области изменения полярного угла, величину диапазона полярного радиуса можно задать произвольным образом непосредственно на графической области так же, как меняется диапазон значений по осям в декартовой системе координат.