Рисунок 17 – УХМ однофазного КЗ.
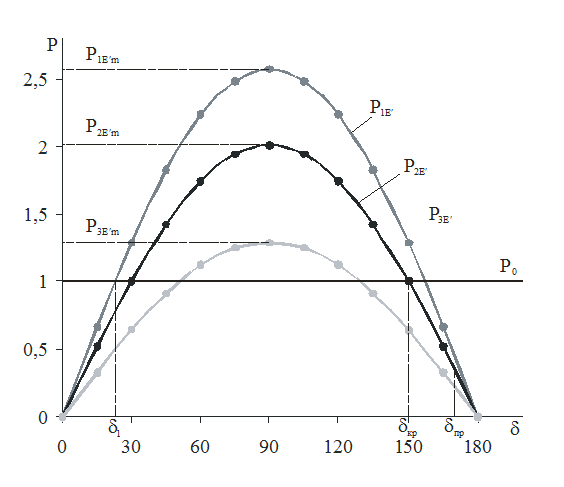
Рисунок 18 – УХМ двухфазного КЗ.
Рисунок 19 – УХМ двухфазного КЗ на землю.
Рисунок 20 – УХМ трехфазного КЗ.
4 АНАЛИЗ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ ПРИ КОРОТКОМ
ЗАМЫКАНИИ НА ЛЭП МЕТОДОМ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
НЕЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Этот метод представляет собой вычислительный эксперимент, проводимый не в реальной системе, а на ее математическом описании (математической модели).
Основное дифференциальное уравнение ротора генератора:
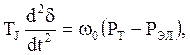 (53)
(53)
где
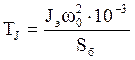 – постоянная инерции эквивалентного
генератора (Jэ определяется в п. 1.3);
– постоянная инерции эквивалентного
генератора (Jэ определяется в п. 1.3);
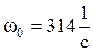 – синхронная скорость;
– синхронная скорость;
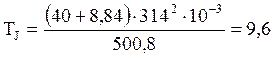 ;
;
РТ – мощность турбины;
РЭЛ – электрическая мощности генератора, зависящая от режима работы системы.
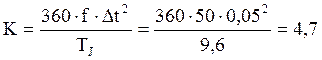 .
.
4.1 Численное интегрирование нелинейного дифференциального уравнения (53) в случае РТ = const
Задачей решения является определение функции δ(t) в переходном процессе.
Выбираем шаг интегрирования ∆t = 0,05с и систему дифференциальных уравнений приводят к схеме вычисления переменных на n-м интервале:
![]() ; (54)
; (54)
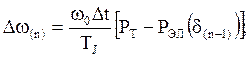 (55)
(55)
![]() (56)
(56)
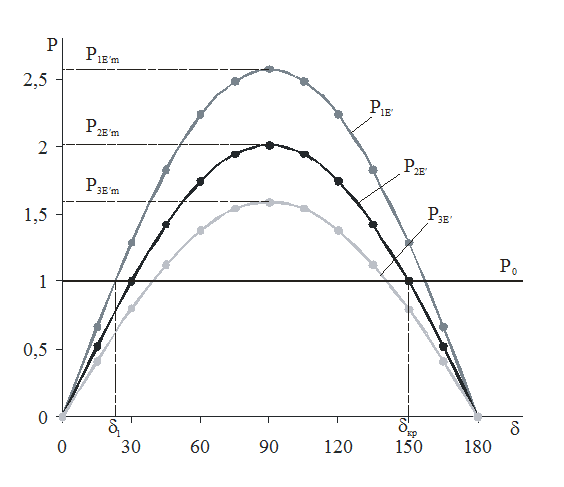
В этот момент возникает КЗ, изменяется угловая характеристика мощности РЭЛ(0) = Р3Е¢(δ1) (по п. 3.3.1) нарушается равенство РТ – РЭЛ = 0, и угол δ начинает увеличиваться. После отключения ЛЭП (tОТКЛ = 0,15 ÷ 0,3с) величину РЭЛ рассчитываем по характеристике УХМ послеаварийного режима Р2Е¢(δ) (по п.3.3.1). Расчет δ(n) проводим до тех пор, пока угол не начнет уменьшаться (в случае динамической устойчивости) или не достигнет критической величины δкр (по п. 3.3.2) – в случае нарушения динамической устойчивости.
4.2 Определение предельного времени отключения КЗ
Предполагая, что КЗ возникает и длится достаточно долго, согласно п.4.1 рассчитывают функцию δ(t) и определяют момент времени tпр , при котором δ(tпр) = δпр (по п. 4.1). Это время tпр и представляет собой предельное время отключения КЗ.
Однофазное КЗ:
δ(0) = 22,89º;
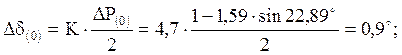
δ(1) = 0,9º + 22,89º = 23,79º;
∆δ(1) =0,9º + 4,7 ∙ (1 – 1,59 ∙ sin 23,79º) = 2,58º;
δ(2) = 2,58º + 23,79º = 26,37º;
∆δ(2) = 2,58º + 4,7 ∙ (1 – 1,59 ∙ sin 26,37º) = 3,96º;
δ(3) = 3,96º + 26,37º = 30,33º;
∆δ(3) = 3,96º + 4,7 ∙ (1 – 1,59 ∙ sin 30,33º) = 4,89º;
δ(4) = 4,89º + 30,33º = 35,22º;
∆δ(4) = 4,89º + 4,7 ∙ (1 – 1,59 ∙ sin 35,22º) = 5,28º;
δ(5) = 5,28º + 35,22º = 40,5º;
∆δ(5) = 5,28º + 4,7 ∙ (1 – 1,59 ∙ sin 40,5º) = 5,13º;
δ(6) = 5,13º + 40,5º = 45,63º;
∆δ(6) = 5,13º + 4,7 ∙ (1 – 1,59 ∙ sin 45,63º) = 4,48º;
δ(7) = 4,48º + 45,63º = 50,11º;
∆δ(7) = 4,48º + 4,7 ∙ (1 – 1,59 ∙ sin 50,11º) = 3,45º;
δ(8) = 3,45º + 50,11º = 53,56º;
∆δ(8) = 3,45º + 4,7 ∙ (1 – 1,59 ∙ sin 53,56º) = 2,14º;
δ(9) = 2,14º + 53,56º = 55,7º;
∆δ(9) = 2,14º + 4,7 ∙ (1 – 1,59 ∙ sin 55,7º) = 0,67º;
δ(10) = 0,67º + 55,7º = 56,37º;
∆δ(10) = 0,67º + 4,7 ∙ (1 – 1,59 ∙ sin 56,37º) = –0,86º;
δ(11) = –0,86º + 56,37º = 55,51º – угол начинает уменьшаться.
Двухфазное КЗ ( 170,17º )
δ(0) = 22,89º;
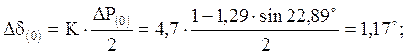
δ(1) = 1,17º + 22,89º = 24,06º;
∆δ(1) =1,17º + 4,7 ∙ (1 – 1,29 ∙ sin 24,06º) = 3,4º;
δ(2) = 3,4º + 24,06º = 27,46º;
∆δ(2) = 3,4º + 4,7 ∙ (1 – 1,29 ∙ sin 27,46º) = 5,3º;
δ(3) = 5,3º + 27,46º = 32,76º;
∆δ(3) = 5,3º + 4,7 ∙ (1 – 1,29 ∙ sin 32,76º) = 6,72º;
δ(4) = 6,72º + 32,76º = 39,49º;
∆δ(4) = 6,72º + 4,7 ∙ (1 – 1,29 ∙ sin 39,49º) = 7,57º;
δ(5) = 7,57º + 39,49º = 47,05º;
∆δ(5) = 7,57º + 4,7 ∙ (1 – 1,29 ∙ sin 47,05º) = 7,83º;
δ(6) = 7,83º + 47,05º = 54,88º;
∆δ(6) = 7,83º + 4,7 ∙ (1 – 1,29 ∙ sin 54,88º) = 7,57º;
δ(7) = 7,57º + 54,88º = 62,45º;
∆δ(7) = 7,57º + 4,7 ∙ (1 – 1,29 ∙ sin 62,45º) = 6,89º;
δ(8) = 6,89º + 62,45º = 69,34º;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.