Х1 = ХГ*б + ХТ1*б, (36)
Х1 = 2,1 + 0,087 = 2,187,
![]()
![]()
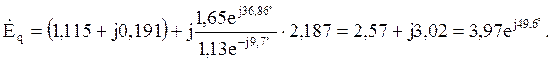
Комплексные значения сопротивлений Z11 и Z10 определяют из схем простейших систем пп.2.1.1, 2.1.2, 2.1.3 с учетом включения сопротивления нагрузки, определенного в п. 1.1, по формулам:
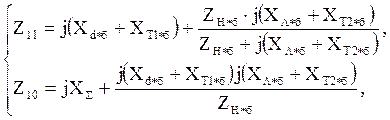 (37)
(37)
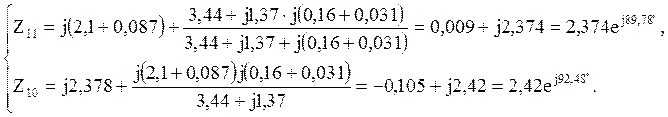
По найденным комплексным сопротивлениям определяют их модули. Углы α11 и α10 рассчитывают по формулам:
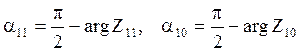 ,
(38)
,
(38)
![]()
Предел передаваемой мощности генератора в сложной системе имеет два значения:
1 – для ЭС – наибольшее значение характеристики УХМ;
2– собственно для передачи – максимум взаимной мощности.
Именно последнее определяет величину предела передаваемой мощности, предела статической устойчивости и коэффициента запаса статической устойчивости, которая необходимо найти.
Предел мощности:
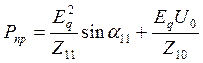 ,
(39)
,
(39)
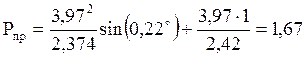 .
.
Предел статической устойчивости δ10 наступает при выполнении условия:
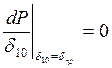 т. е. при δпр.
= 90о + α10,
(40)
т. е. при δпр.
= 90о + α10,
(40)
δпр. = 90о + (–2,48о) = 87,8о.
Коэффициент запаса статической устойчивости:
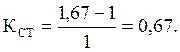
2.2.2 Неявнополюсный генератор с регулятором пропорционального действия.
Генератор вводится в схему замещения э.д.с. Е'q и сопротивлением Х'd. Вычисление Е'q проводим следующим образом:
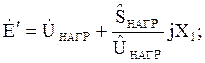 (41)
(41)
![]()
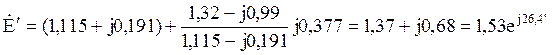 ;
;
![]() ;
;
δ10 = arg Eq; δ'10 = arg E';
δ10 = 49,5º; δ'10 = 26,4º';
E'q = E' cos (δ10 - δ'10); (42)
E'q = 1,53 · cos(49,5 – 26,4) = 1,41.
Предел мощности и предел устойчивости вычислить аналогично п. 2.2.1, приняв вместо Eq и Хd*6 соответственно E'q и Х′d*6.
Комплексные значения сопротивлений Z11 и Z10:
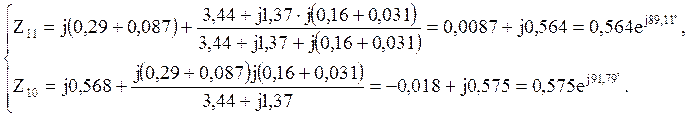
Углы α11 и α10 :
![]() .
.
Предел мощности:
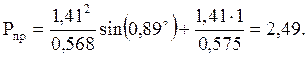
Предел статической устойчивости δ10 наступает при выполнении условия:
δпр. = 90о + (–1,79о) = 88,21о.
Коэффициент запаса статической устойчивости:
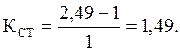
2.2.3 Неявнополюсный генератор с регулятором сильного действия.
Генератор вводится в схему замещения напряжением UГq и сопротивлением равным нулю.
Вычисление UГq производим следующим образом:
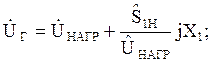 (43)
(43)
![]()
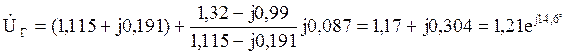 ;
;
![]() ;
;
![]() ;
;
UГq = UГ cos(δ10 - δ1С). (44)
Uгq=1,21∙cos(49,5 – 14,6)=0,992
Предел мощности и предел устойчивости вычислить аналогично п. 2.2.1, приняв вместо Eq и Хd*6 соответственно UГq и 0.
Комплексные значения сопротивлений Z11 и Z10:
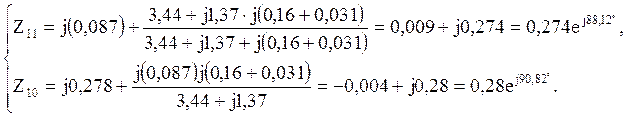
Углы α11 и α10 :
![]() .
.
Предел мощности:
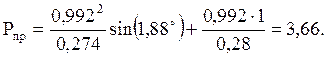
Предел статической устойчивости δ10 наступает при выполнении условия:
δпр. = 90о + (–0,82о) = 89,18о.
Коэффициент запаса статической устойчивости:
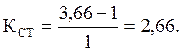
2.3 Выводы
Полученные результаты представляем в виде таблицы.
Таблица 6.
|
Наличие и тип АРВ |
Рпр |
δпр |
КСТ |
|||
|
без нагр. |
с нагр. |
без нагр. |
с нагр. |
без нагр. |
с нагр. |
|
|
Без АРВ |
1,43 |
1,67 |
90 |
87,8 |
0,43 |
0,67 |
|
С АРВ пропорционального типа |
2,7 |
2,49 |
112,9 |
88,21 |
1,7 |
1,49 |
|
с АРВ сильного действия |
4,6 |
3,66 |
118,24 |
89,18 |
3,6 |
2,66 |
3 АНАЛИЗ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ
СИСТЕМЫ МЕТОДОМ ПЛОЩАДЕЙ
В расчетах динамической устойчивости генератор вводится сопротивлением Х′d и э.д.с. E' независимо от наличия или отсутствия АРВ для исходного и всех последующих режимов, а характеристика УХМ имеет вид:
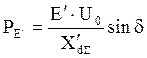 .
(45)
.
(45)
Исходный режим определяется (п. 2.1.1) передачей мощности без учета нагрузки, э.д.с. E' берем из п. 2.1.2, характеристику УХМ определяем по (45); угол δ1 исходного режима:
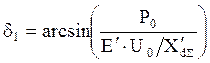 ,
(46)
,
(46)
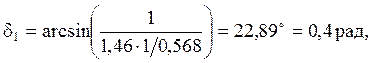
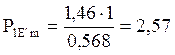
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.