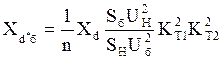Определение предела передаваемой мощности передачи и влияния нагрузки и АРВ на этот параметр. Анализ динамической устойчивости электроэнергетической системы методом площадей, страница 2

.                                                       (4)

.

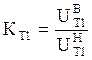Для трансформаторов мощностью 125 МВА:

.

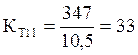Для трансформатора мощностью 630 МВА:

.

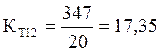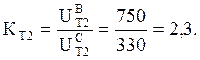
Относительное сопротивление для нерегулируемых генераторов мощностью 63 кВт:

.

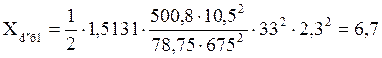Относительное сопротивление для нерегулируемого генератора мощностью 500 кВт:

.

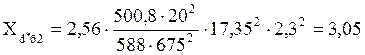Относительное сопротивление генератора с АРВ пропорционального действия:

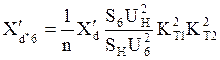                                                      (5)

Относительное сопротивление для генераторов с АРВ мощностью 63 кВт:

.

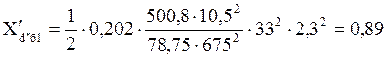Относительное сопротивление для генератора с АРВ мощностью 500 кВт:

.

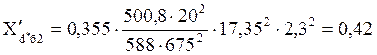Относительное сопротивление трансформатора:

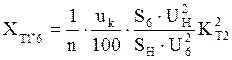.                                                       (6)

Относительное сопротивление для трансформаторов мощностью 125 МВА:

.

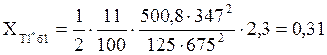Относительное сопротивление для трансформатора мощностью 630 МВА:

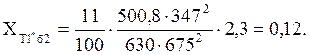
Относительное сопротивление линии:

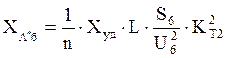,                                              (7)

где Х_уд = 0,4 Ом/км – удельное сопротивление линии.

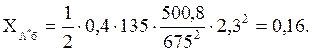
Относительное сопротивление автотрансформатора:

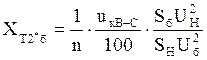,                                                        (8)

.

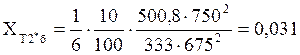Относительное сопротивление нагрузки:

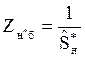                                                                   (9)

где – сопряженный комплекс мощности нагрузки.

где

;      

,

,

.

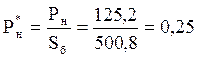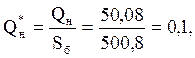
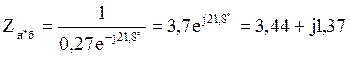В дальнейших расчетах индекс «*» при соответствующих величинах опускаем, т.к. действия проводятся только с относительными базисными величинами. В приведенных формулах n – это число параллельно включенных соответствующих элементов.

1.3 Определение параметров эквивалентного генератора

Пренебрегая взаимным движением ротора турбогенераторов ЭС и учитывая движение роторов генераторов ЭС только относительно ротора эквивалентного генератора ШСБМ, заменяют агрегаты ЭС эквивалентными параметрами:

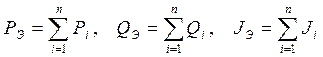                                              (10)

где P_э Q_э J_э – активная и реактивная мощности, и момент инерции эквивалентного агрегата;

P_i Q_i J_i – активные и реактивные мощности, и моменты инерции отдельных блоков ЭС.

Схема замещения с нерегулируемыми генераторами имеет вид:

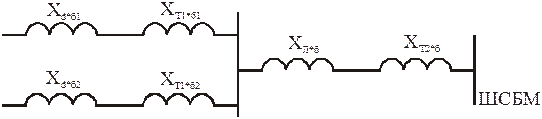
Рисунок 2.

Упрощаем схему:

;

;

;

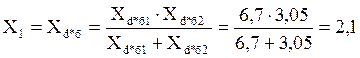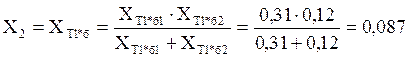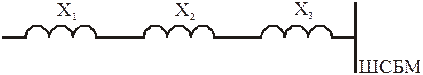
Рисунок 3.

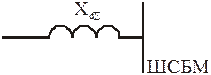
Рисунок 4.

Схема замещения с генераторами с АРВ пропорционального действия имеет вид:

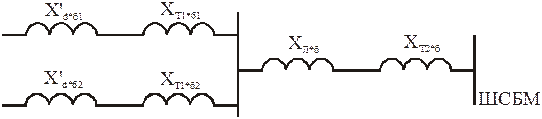
Рисунок 5.

;

;      ;

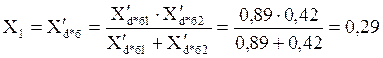Рисунок 6.

Рисунок 7.

Переходим к относительным единицам:

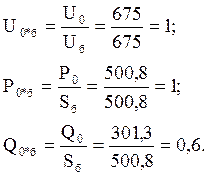
2 ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ ПЕРЕДАЧИ

И ВЛИЯНИЯ НАГРУЗКИ И АРВ НА ЭТОТ ПАРАМЕТР

2.1 Определение предела передаваемой мощности (ППМ) при отсутствии нагрузки.

При отсутствии нагрузки ЭЭС является простейшей.

2.1.1 Генераторы ЭС, не имеющие АРВ вводят в схему замещения сопротивлениями Х_d. Схему замещения сворачивают относительно ШСБМ и определяют суммарное сопротивление передачи Х_d∑.

Х_d∑ = Х_d*б + Х_с,                                                     (11)

где Х_с – сопротивление связи генераторов с системой.

Х_с = Х_Т1*б + Х_Т2*б + Х_Л*б,                                                      (12)

Х_с = 0,087+0,031 + 0,16 = 0,278,

Х_d∑ = 2,1 + 0,278 = 2,378.

По известным P₀ и Q₀ рассчитывают э.д.с. эквивалентного генератора Е_q:

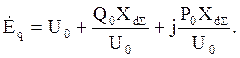                                                                (13)

Модуль э.д.с. Е_q определяют по формуле:

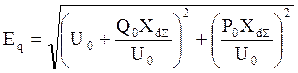,                                       (14)

.

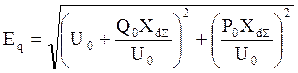Аргумент:

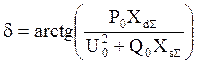,                                                  (15)

,

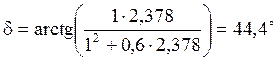Угловая характеристика мощности (УХМ):

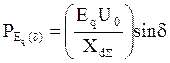,                                                   (16)

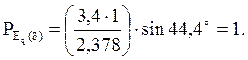
Предел передаваемой мощности:

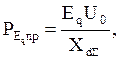                                                        (17)

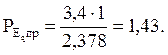
Предел статической устойчивости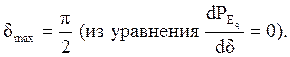

Коэффициент запаса статической устойчивости:

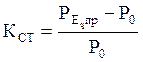,                                                    (18)

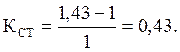
2.1.2 Генераторы ЭС и АРВ пропорционального действия вводятся в схему замещения сопротивлениями Х¢_d. Далее расчет аналогичен расчету 2.1.1.

Рассчитывают э.д.с. :

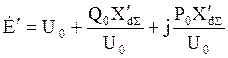                                                     (19)

где  – суммарное сопротивление передачи:

,                                                     (20)

Из равенства (19) модуль эдс: