Лекция 17. Расчет установившейся ошибки в системах управления. Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: ![]() , рисунок 116.
, рисунок 116.

Очевидно, установившаяся ошибка зависит от законов изменения и численных характеристик входных сигналов системы. Поэтому при ее определении принято рассматривать так называемые типовые входные сигналы, законы изменения которых составляют степенной ряд относительно времени. Например, для задающего воздействия:
![]() ,
, ![]() ,
,  и так
далее.
и так
далее.
При наличии нескольких воздействий на линейную систему для определения xуст используется принцип суперпозиции – реакция линейной системы на совокупность входных сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в отдельности:
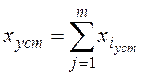 , где
каждое слагаемое, или составляющая сигнала ошибки,
, где
каждое слагаемое, или составляющая сигнала ошибки, ![]() определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
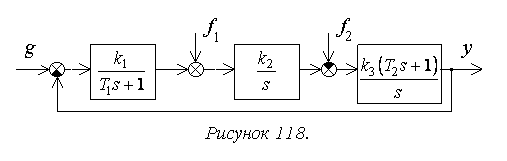
Рассмотрим порядок расчета установившейся ошибки на следующем достаточно общем примере (рисунок 117).
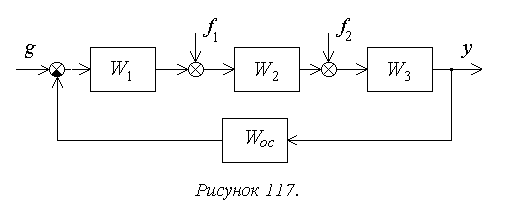
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих ![]() .
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке ![]() при известном изображении задающего
воздействия G(s):
при известном изображении задающего
воздействия G(s):
![]() , где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
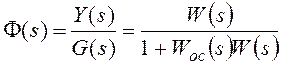 , где
, где ![]() - передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
- передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета установившегося значения ошибки от задающего воздействия используют теорему о конечном значении для преобразования Лапласа:
![]()
В результате:
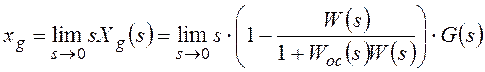 .
.
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения ![]() при известном изображении возмущающего
воздействия F(s):
при известном изображении возмущающего
воздействия F(s):
![]() , где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
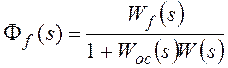 ;
;
Wf(s) – передаточная функция разомкнутой системы по возмущению (передаточная функция участка прямой цепи системы от точки приложения возмущающего воздействия до выхода системы).
Для структурной схемы на рисунке 8 необходимо учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
![]() ,
,
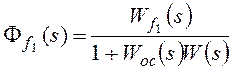 ,
,
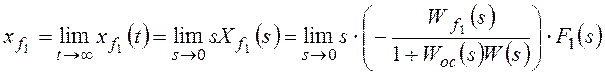 .
.
Для f2:
![]() ,
,
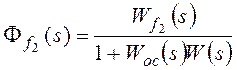 ,
,
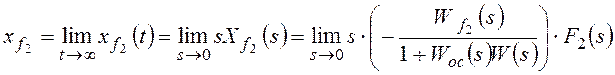 .
.
Расчет упрощается для системы с единичной отрицательной обратной связью (рисунок 118):
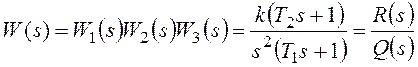 ,
,
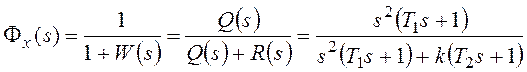 , где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
, где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
Найдем установившуюся ошибку для некоторых типовых вариантов задающего воздействия.
При ![]() получим:
получим:
![]()
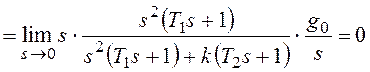 .
.
При ![]() получим:
получим:
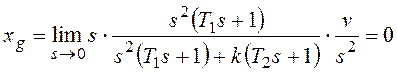 .
.
При  получим:
получим:
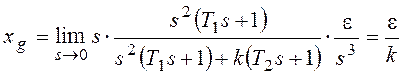 .
.
Если установившаяся ошибка тождественно равна нулю при каком-либо типовом варианте входного сигнала, независимо от его численных характеристик, систему называют астатической по рассматриваемому входному сигналу.
Количество типовых вариантов входного сигнала – членов степенного ряда, при которых установившаяся ошибка тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся ошибку от возмущения f1:
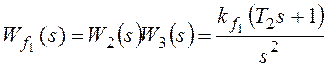 ,
,
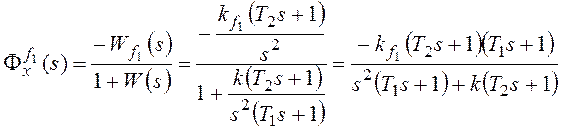 , где
, где ![]() –
коэффициент передачи разомкнутой системы по возмущению f1.
–
коэффициент передачи разомкнутой системы по возмущению f1.
При ![]() получим:
получим:
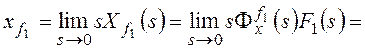
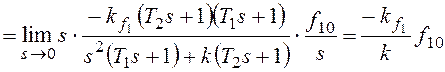 .
.
При ![]() получим:
получим:
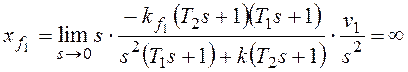 .
.
При 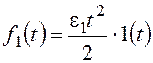 получим
тот же результат.
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система не является астатической. Кроме того, она не в состоянии отработать два последних варианта входного сигнала.
Рассмотрим установившуюся ошибку от возмущения f2:
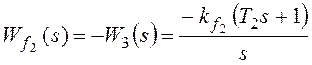 ,
,
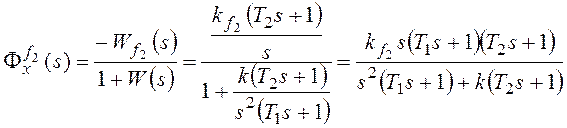 , где
, где ![]() –
коэффициент передачи разомкнутой системы по возмущению f2.
–
коэффициент передачи разомкнутой системы по возмущению f2.
При ![]() получим:
получим:
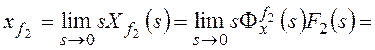
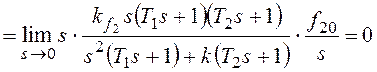 .
.
При ![]() получим:
получим:
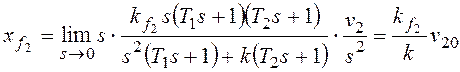 .
.
При 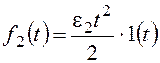 получим:
получим:
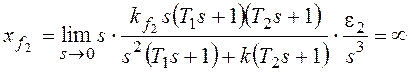 .
.
По возмущению f2 рассматриваемая система имеет астатизм первого порядка. Она не в состоянии отработать возмущающее воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени звеньев системы не влияют на ее точность.
3. Увеличение значения коэффициента передачи разомкнутой системы приводит к снижению величины установившейся ошибки.
Для систем с единичной отрицательной обратной связью существуют достаточно простые структурные признаки астатизма.
Рассмотрим структуру, показанную на рисунке 119.
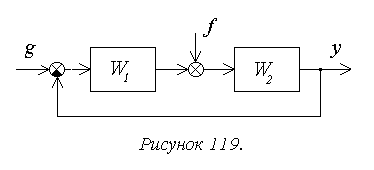
В общем случае передаточная функция разомкнутой системы может быть представлена в следующей форме:
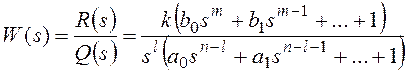 , где l³0.
, где l³0.
Тогда получим:
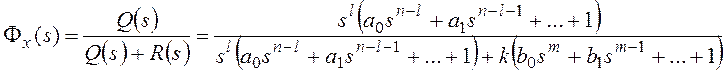
и для общего вида задающего воздействия 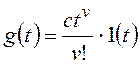 , которому соответствует изображение
, которому соответствует изображение 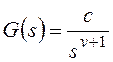 ,
,
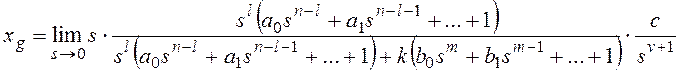 .
.
Результат нахождения этого предела зависит от соотношения показателей степени:
- при l>v установившаяся ошибка равна нулю независимо от остальных параметров, то есть имеет место астатизм;
- при l=v получаем константу;
- при l<v установившаяся ошибка стремится к бесконечности, то есть система не в состоянии отработать входной сигнал.
Учитывая, что минимальное значение v нулевое, получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный признак астатизма по задающему воздействию в системе с единичной отрицательной обратной связью состоит в наличии нулевых корней в знаменателе передаточной функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться, что положительное значение l совпадает с порядком астатизма.
Для получения признака астатизма по возмущающему воздействию представим передаточные функции на рисунке 10 в форме:
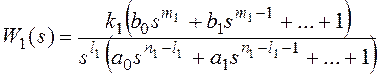 ,
,
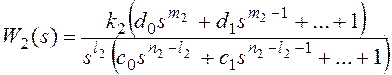 , где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем
, где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем ![]() и
и ![]() .
.
Тогда получим:
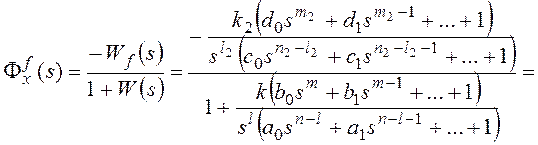
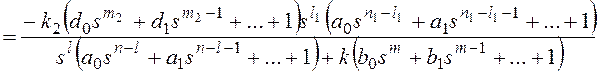
и для общего вида возмущающего воздействия 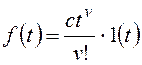 , которому соответствует изображение
, которому соответствует изображение 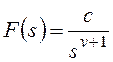 ,
,
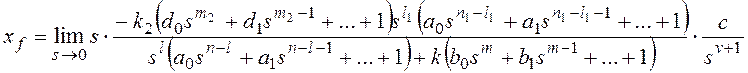 .
.
Все вышеприведенные выводы можно повторить для показателя степени l1.
Таким образом, структурный признак астатизма по возмущающему воздействию в системе с единичной отрицательной обратной связью состоит в наличии нулевых корней в знаменателе передаточной функции участка системы до точки приложения воздействия, или интегрирующих звеньев на том же участке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.