Лекция 18.Синтез систем управления
Существуют два основных принципа синтеза систем управления:
- построение системы с обеспечением заданных требований к показателям ее качества;
- построение системы, характеристики которой оптимальны в некотором смысле.
Для реализации первого принципа известны различные методы:
- корневой метод;
- метод корневого годографа;
- метод стандартных переходных характеристик;
- метод логарифмических амплитудных характеристик.
Для реализации второго принципа используется математический аппарат вариационного исчисления и принцип максимума или метод динамического программирования.
Подробно рассмотрим метод логарифмических амплитудных характеристик, наиболее широко применяемый на практике.
Основной вариант этого метода основан на использовании асимптотической ЛАХ разомкнутой системы. При этом система должна быть минимально-фазовой, то есть передаточная разомкнутой системы не должна содержать нулей (корней числителя) и полюсов (корней знаменателя) в правой полуплоскости.
Процесс синтеза в соответствии с методом ЛАХ включает в себя следующие основные этапы:
1. Построение исходной ЛАХ L(w) – асимптотической ЛАХ разомкнутой нескорректированной системы, включающей в себя объект управления, устройство управления, соответствующее цели управления, но, возможно, не обеспечивающее требуемого качества, необходимые измерительные устройства. Пример – следящая система с П-регулятором.
2. Построение желаемой ЛАХ Lж(w) на основе требований к показателям качества системы.
3. Нахождение асимптотической ЛАХ последовательного корректирующего устройства:
![]() .
.
4. Получение на основе Lпку(w) передаточной функции корректирующего устройства и выбор способа его реализации: в виде дополнительного звена в прямой цепи (ПКУ), эквивалентного параллельного корректирующего звена, обратной связи или построение нового устройства управления, возможно, компьютерного.
При построении желаемой ЛАХ, как правило, рассматриваются требования к точности и запасу устойчивости системы.
При использовании первого принципа, как правило, требуется обеспечить заданные точность и запас устойчивости системы. При этом требования к точности определяют вид и характеристики желаемой ЛАХ на низких частотах. Требования к запасу устойчивости – на средних частотах (в окрестности частоты среза).
Вспомним приближенное соотношение для оценки точности
системы при гармоническом входном сигнале ![]() :
:
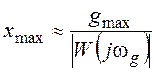 , (3.1)
, (3.1)
где xmax – амплитуда сигнала ошибки, W(jw) – частотная передаточная функция разомкнутой системы.
|
Рисунок 11. |
Формула (3.1) позволяет установить требования к низкочастотной части ЛАХ разомкнутой системы. Для того, чтобы максимальная ошибка замкнутой системы при гармоническом воздействии не превышала заданного значения emax, ЛАХ разомкнутой системы должна проходить выше контрольной точки с координатами (рисунок 11):
w = wg, 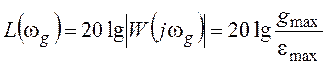 . (3.2)
. (3.2)
В общем случае требования к точности системы включают в себя требуемый порядок астатизма и допустимую амплитуду сигнала ошибки emax для входного сигнала произвольного вида, в том числе случайного.
Первое требование определяет наклон первого участка асимптотической ЛАХ: для астатизма 1-го порядка -20 дБ/дек, 2-го порядка -40 дБ/дек и так далее.
Второе требование можно учесть, если известны
максимально возможные значения первой производной (скорости) 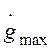 и второй производной (ускорения)
и второй производной (ускорения) 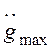 входного сигнала. Для заданных значений
этих характеристик можно подобрать эквивалентный гармонический сигнал
входного сигнала. Для заданных значений
этих характеристик можно подобрать эквивалентный гармонический сигнал ![]() из условий:
из условий: 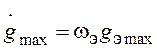 и
и 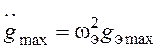 . В результате можно получить:
. В результате можно получить:
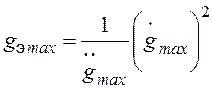 ,
, 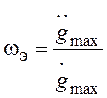 . (3.3)
. (3.3)
Теперь при заданной максимальной допустимой ошибке emax в соответствии с (3.2) могут быть получены координаты контрольной точки:
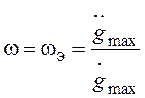 ,
, 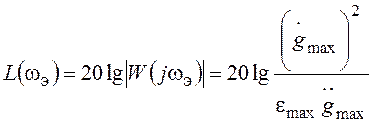 .
.
Если для эквивалентного гармонического сигнала
предположить, что 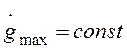 , а
, а 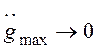 , то при
уменьшении
, то при
уменьшении 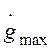 в 10 раз эквивалентная частота уменьшится
в 10 раз, а значение L(wэ) увеличится на 20 дБ, то есть контрольная точка будет
смещаться влево по прямой с наклоном -20 дБ/дек. В пределе получим
режим работы системы при задающем воздействии вида
в 10 раз эквивалентная частота уменьшится
в 10 раз, а значение L(wэ) увеличится на 20 дБ, то есть контрольная точка будет
смещаться влево по прямой с наклоном -20 дБ/дек. В пределе получим
режим работы системы при задающем воздействии вида 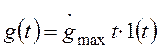 , и
заданные значения
, и
заданные значения 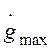 и emax будут определять требуемое значение коэффициента
передачи системы с астатизмом первого порядка (добротность по скорости):
и emax будут определять требуемое значение коэффициента
передачи системы с астатизмом первого порядка (добротность по скорости):
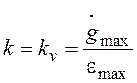 .
.
|
Рисунок 12. |
Если для эквивалентного гармонического сигнала
предположить, что 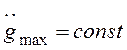 , а
, а 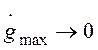 , то
аналогично можно показать, что контрольная точка будет смещаться вправо по
прямой с наклоном - 40 дБ/дек.
, то
аналогично можно показать, что контрольная точка будет смещаться вправо по
прямой с наклоном - 40 дБ/дек.
Область, расположенная ниже двух таких прямых должна рассматриваться как запретная область для ЛАХ синтезируемой системы (рисунок 12). Это обеспечит заданную точность при известных максимальных значениях скорости и ускорения входного сигнала.
Полученной запретной области может соответствовать только астатическая система. Распространение полученных результатов на статические системы может быть выполнено, если принять ограничение не только на скорость и ускорение, но и на величину задающего воздействия gmax.
Подберем эквивалентный гармонический сигнал из
условий: ![]() ,
, 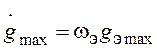 . Тогда
при заданной допустимой ошибке emax получим контрольную точку с координатами:
. Тогда
при заданной допустимой ошибке emax получим контрольную точку с координатами:
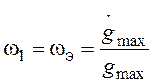 ,
, 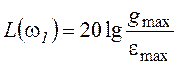 .
.
|
Рисунок 13. |
Если уменьшать 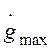 при
постоянной gmax, контрольная точка будет сдвигаться влево по
горизонтальной прямой на уровне
при
постоянной gmax, контрольная точка будет сдвигаться влево по
горизонтальной прямой на уровне 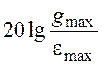 , а при уменьшении gmax при постоянной
, а при уменьшении gmax при постоянной 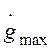 - вправо по прямой с с наклоном -20дБ/дек, пока будет выполняться условие
- вправо по прямой с с наклоном -20дБ/дек, пока будет выполняться условие 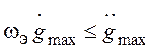 . Далее
следует воспользоваться полученными выше результатами. После частоты
. Далее
следует воспользоваться полученными выше результатами. После частоты 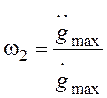 получим прямую с наклоном - 40 дБ/дек.
Таким образом, если не требуется обеспечить астатизм системы, то при условии
ограничения максимальной величины задающего воздействия запретная область для
ЛАХ разомкнутой системы будет иметь вид, показанный на рисунке 13.
получим прямую с наклоном - 40 дБ/дек.
Таким образом, если не требуется обеспечить астатизм системы, то при условии
ограничения максимальной величины задающего воздействия запретная область для
ЛАХ разомкнутой системы будет иметь вид, показанный на рисунке 13.
Требования к запасу устойчивости системы в рамках метода ЛАХ задаются в форме максимально допустимой величины показателя колебательности.
По заданному значению M=Mmax на рисунке 14 построена запретная область для амплитудно-фазовой частотной характеристики (рисунок 14а) или ЛФЧХ (рисунок 14б) разомкнутой системы.
|
Рисунок 14. |
Для рисунке 14б границы запретной области вдоль оси частот соответствуют расстояниям от начала координат до точек пересечения окружности (рисунок 14а) с отрицательной вещественной полуосью:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.