Основные формы математического описания систем управления: структурно-динамическая схема

Лекция 2. Основные формы математического описания систем управления: структурно-динамическая схема

В качестве основных выделим следующие формы математического оптсания систем управления:

1. Структурно-динамическая схема.

2. Передаточные функции.

3. Общие дифференциальные уравнения.

4. Система дифференциальных уравнений.

5. Векторно-матричная форма.

Структурно-динамическая схема

При составлении математической модели система разбивается на динамические звенья. Для них составляются математические модели. После этого динамические звенья объединяются в структурно-динамическую схему.

Структурно-динамическая схема (структурная схема) системы отражает динамические свойства отдельных звеньев системы и их взаимодействие.

Динамическое звено – это устройство любой физической природы и любого конструктивного исполнения, описываемое дифференциальным уравнением определенного вида. То есть главное здесь – конкретное математическое описание. Именно с математическими моделями работает теория управления. Поэтому математическая модель звена или системы должна правильно отображать их свойства, существенные с точки зрения решаемой задачи.

Здесь полезно привести два примера:

Электрическая схема, электрический двигатель, кастрюля с супом, летательный аппарат, студенческая аудитория и пр. при определенных допущениях, определяемых условиями задачи, оказываются одним и тем же динамическим звеном, то есть демонстрируют аналогичные динамические свойства. Формально это определяется тем, что для всех этих объектом может быть получено одно и то же дифференциальное уравнение (различие может быть только в численных значениях коэффициентов).

Для одного и того же реального объекта могут быть составлены разные модели динамического звена – тоже в зависимости от условий задачи и допущений.

Фундаментальным свойством динамического звена является направленность действия. То есть с формальной точки зрения динамическое звено преобразует свои входные сигналы в выходные и ни в коем случае не наоборот.

Под входными сигналами понимают конкретные физические параметры, характеризующие воздействие на динамическое звено предшествующих по структурной схеме системы звеньев или внешней среды. Под выходными сигналами понимают конкретные физические параметры, характеризующие воздействие рассматриваемого звена на последующие по структурной схеме системы звенья.

В соответствии со сказанным для динамического звена используются условные обозначения, показанные на рисунке 15: а) звено с одним входом и одним выходом; б) звено с двумя входами и тремя выходами.

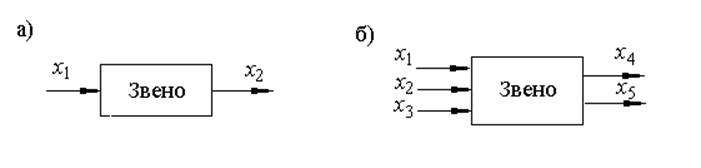
Рисунок 15.

Свойство направленности действия можно сформулировать несколько иначе: характеристики преобразования звеном входных сигналов не зависят от характеристик последующих звеньев, от их наличия или отсутствия.

Разбивать систему на динамические звенья необходимо так, чтобы каждое звено обладало свойством направленности действия. Поэтому часто структура модели отличается от функциональной схемы системы, отражающей состав реальных элементов. Если отдельные элементы системы не обладают рассматриваемым свойством, они могут разбиваться на динамические звенья или объединяться в них.

Для динамического звена используются две основные формы математической модели: дифференциальное уравнение (в простейших случаях - алгебраическое) и передаточная функция.

Дифференциальное уравнение является универсальной формой модели динамического звена. Передаточная функция в строгом смысле может применяться только для линейных звеньев.

Дифференциальное уравнение должно составляться в строгом соответствии со следующими правилами:

1. В дифференциальном уравнении звена должны присутствовать только входные и выходной сигнал (при наличии нескольких выходных сигналов для каждого составляется отдельное уравнение).

2. В левой части уравнения должны присутствовать только выходной сигнал и его производные, в правой – входные сигналы и их производные.

3. В левой части уравнения выходной сигнал должен иметь коэффициент единица. Если присутствуют только производные выходного сигнала, коэффициент единица должен быть при низшей производной.

Передаточная функция звена или системы – это отношение изображений по Лапласу его выходного и входного сигналов (рисунок 15а) при нулевых начальных условиях и отсутствии других входных сигналов:

.

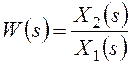В соответствии с этим определением можно сделать вывод, что при наличии нескольких входных и выходных сигналов для рассматриваемого звена или системы должен рассматриваться набор передаточных функций – от каждого входа к каждому выходу. Так для звена с тремя входами и двумя выходами (рисунок 15б) должны быть получены шесть передаточных функций – от каждого входа к каждому выходу.