Основные понятия теории управления и радиоавтоматики. Фундаментальные принципы управления. Классификация систем управления. Общая характеристика задач анализа и синтеза систем

Лекция 1. Основные понятия теории управления и радиоавтоматики. Фундаментальные принципы управления. Классификация систем управления. Общая характеристика задач анализа и синтеза систем

Основное содержание теории управления составляют математические методы анализа и синтеза систем. Основные задачи анализа - исследование свойств системы, прежде всего, устойчивости (в большинстве случаев неустойчивая система неработоспособна) и оценка показателей ее качества. Основные задачи синтеза – корректировка существующей системы или построение новой системы в соответствии с требованиями к ее свойствам и качеству.

Управление - это организованное воздействие на объект с целью обеспечения требуемого течения процесса в объекте или требуемого изменения его состояния.

Рисунок 1 графически интерпретирует это понятие.

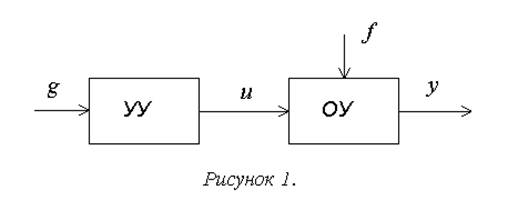
На рисунке 1:

ОУ – объект управления;

y – выходной сигнал, характеризующий текущее состояние объекта управления;

g – задающее воздействие, описывающее требуемое состояние объекта управления (цель управления);

 u – сигнал управления;

УУ – устройство управления (регулятор);

f – возмущающее воздействие – нерегулируемое воздействие внешней среды.

Классификация систем управления определяет выбор используемого математического аппарата и проводится по нескольким признакам. Мы ограничимся основными из них.

1. По принципу управления различают:

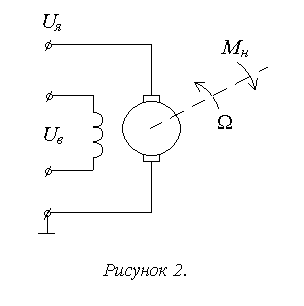
1а. Разомкнутые системы, общая структура которых соответствует рисунку 1. Конкретный пример представлен на рисунке 2. Здесь управляющий сигнал формируется в зависимости только от задающего воздействия. При появлении возмущающего воздействия разомкнутая система управления на него никак не реагирует, что приводит к непредсказуемому отклонению состояния объекта от требуемого. Поэтому разомкнутая система управления сама по себе неработоспособна.

1б. Замкнутые системы, реализующие управление на основе принципа обратной связи – формирование сигнала управления на основе сравнения текущего состояния объекта управления с требуемым (рисунок 3).

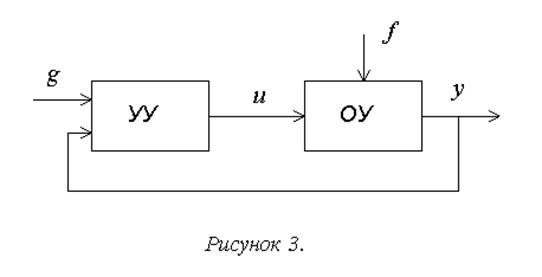
Простейший и основной вариант реализации принципа обратной связи – жесткая единичная отрицательная обратная связь. В этом случае сигнал управления формируется в соответствии с уравнением:

u(t)=k(g(t) – y(t)).                                             (1.1)

Примеры замкнутых систем представлены на рисунках 4, 5.

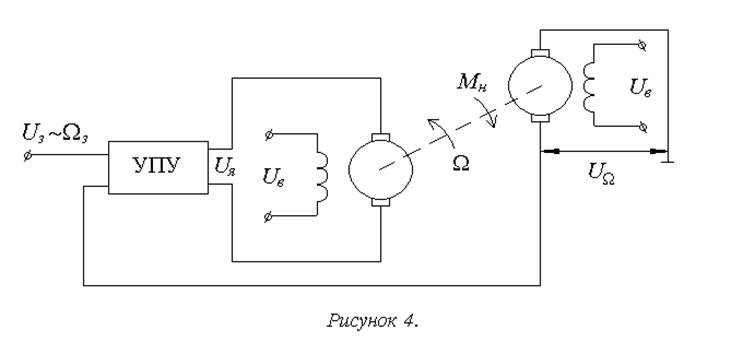
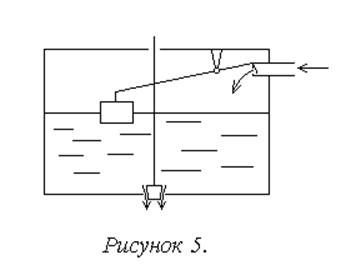
Более подробная классификация замкнутых систем проводится по виду обратной связи.

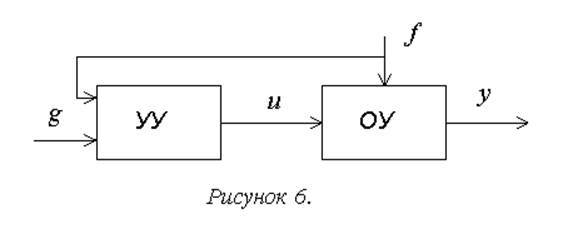
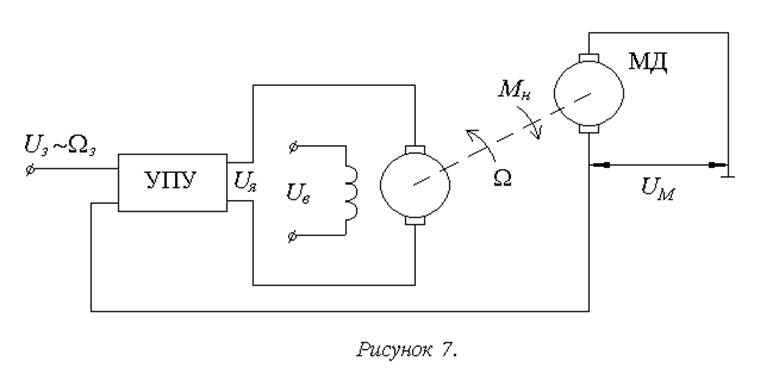
1в. Системы с компенсацией возмущения. Принцип компенсации возмущающего воздействия предусматривает измерение или оценку (идентификацию) величины возмущающего воздействия и использование этой информации для формирования управляющего сигнала (рисунки 6, 7)

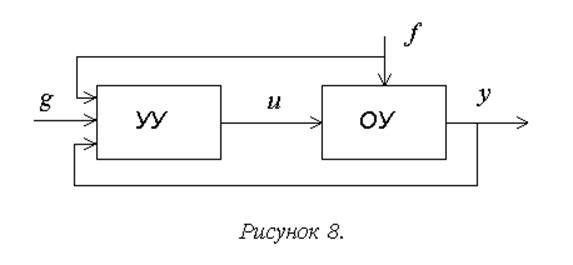
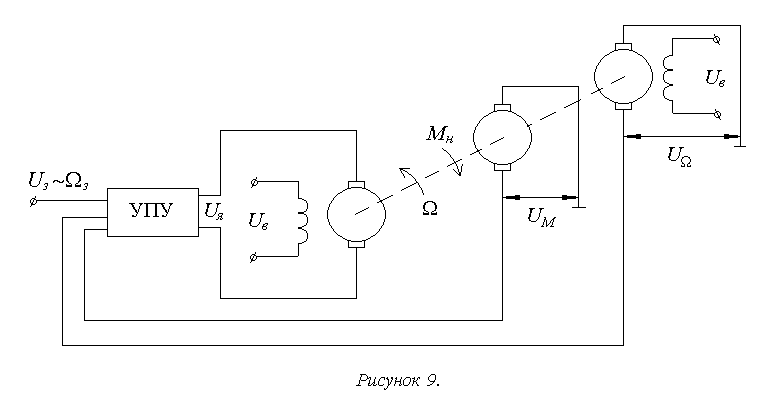
1г. Системы комбинированного управления реализуют сочетание рассмотренных выше принципов. Наиболее распространенный вариант – замкнутая система с компенсацией возмущения (рисунки 8,9).

1д. Адаптивные системы. Принцип адаптивного управления состоит в накоплении в процессе работы системы информации о поведении объекта управления и характеристиках внешней среды и использовании этой информации для корректировки структуры и параметров закона управления (настройки устройства управления).

2. По цели управления различают:

2а. Системы стабилизации:g=const. К их числу относятся все рассмотренные примеры.

2б. Системы программного управления: g= g(t). Пример – система управления ракетой-носителем. При выведении спутника на заданную орбиту законы изменения высоты, скорости, направления движения и пр. рассчитываются заранее. Задачей системы управления является обеспечение их изменения по заданным законам.

2в. Следящие системы: g=var. Пример – система управления антенной радиолокационной станции наблюдения за воздушной обстановкой. Задачей системы является обеспечение совмещения оси антенны с летательным аппаратом при заранее неизвестном законе его движения.

2г. Системы терминального управления. Пример – система самонаведения ракеты. Задачей системы является обеспечение минимального расстояния от ракеты до цели (промаха) в определенный конечный момент времени.

2д. Системы экстремального управления. Такие системы строят, когда в процессе управления требуется обеспечить максимум или минимум некоторых показателей (критериев оптимальности). Пример – система мягкой посадки космического летательного аппарата. Задачей системы является обеспечение мягкой посадки при заранее неизвестных начальных скорости и высоте с минимальным расходом топлива.

3. По структуре различают одномерные (со скалярными входными сигналами) и многомерные (с векторными входными сигналами) системы управления.

4. По форме математического описания различают линейные и нелинейные системы.

4а. Линейной является системы, для всех элементов которой может быть получено математическое описание в форме линейных алгебраических или дифференциальных уравнений.

4б. Если хотя бы один элемент системы не может быть описан линейным уравнением, вся система рассматривается как  нелинейная.