Основные формы математического описания систем управления: структурно-динамическая схема, страница 2

Переход от дифференциального уравнения звена к передаточной функции основан на свойстве линейности преобразования Лапласа и теореме дифференцирования. Содержащееся в определении передаточной функции требование учета нулевых начальных условий упрощает выражение для изображения производной. Оператор Лапласа при нулевых начальных условиях приобретает смысл символа дифференцирования.

Для отображения динамических свойств звеньев на структурной схеме принято использовать передаточные функции.

Рассмотрим пример составления модели следящей системы (рисунок 16).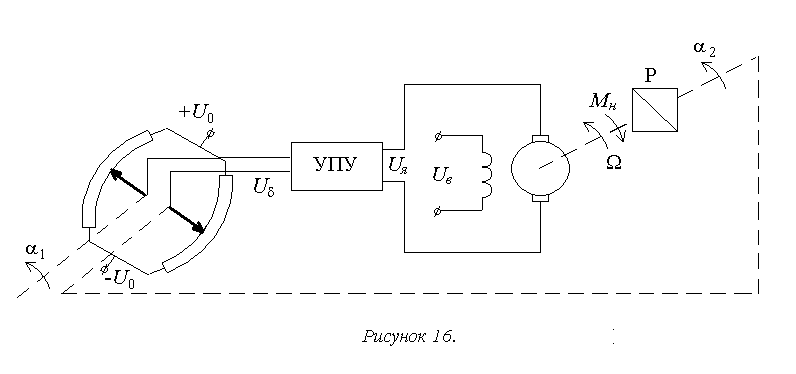

В рассматриваемой системе задающим воздействием является угол поворота входного вала g=a₁, выходным сигналом – угол поворота выходного вала y=a₂. В системе также присутствует возмущающее воздействие f=M_н.

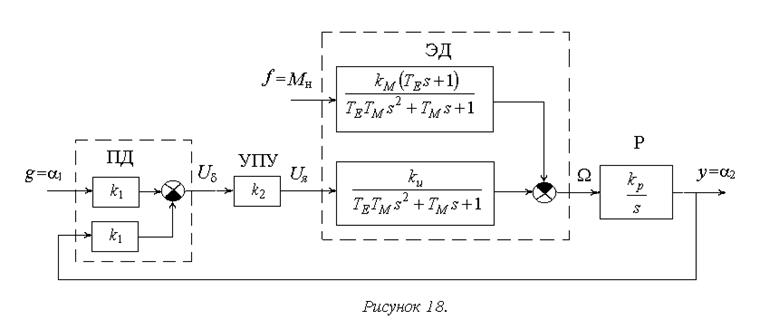
Разобьем систему на динамические звенья и выберем для них входные и выходные сигналы (рисунок 17). Примем, что свойство направленности действия у всех звеньев электрической природы обеспечено большой величиной сопротивления нагрузки, у звеньев механической природы – учетом массы всей вращающейся части в уравнениях двигателя посредством приведенного момента инерции.

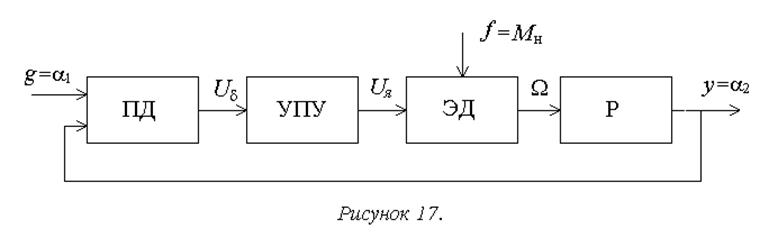
Составим уравнения отдельных звеньев.

Потенциометрический датчик (ПД) при достаточно большом входном сопротивлении усилительно-преобразовательного устройства описывается линейным алгебраическим уравнением:

U_d=k₁(a₁-a₂), которое остается линейным и после перехода к изображениям по Лапласу.

В результате для ПД получаем две передаточные функции – для каждого из входных сигналов:

,     .

Для усилительно-преобразовательного устройства описание аналогично.

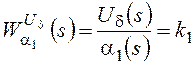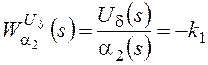U_я=k₂U_d,

.

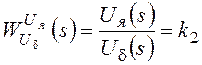Для электродвигателя (ЭД) запишем уравнение равновесия напряжений в цепи якоря:

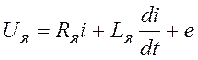                                          (2.1)

и равновесия моментов на валу двигателя:

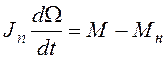.                                         (2.2)

В уравнениях (2.1)-(2.2): i – ток в якоре двигателя; R_я – активное сопротивление цепи якоря; L_я – индуктивность цепи якоря; e=c_eW - противо-ЭДС, генерируемая на катушке якоря за счет его вращения в магнитном поле; J_п – приведенный момент инерции вала двигателя вместе с выходным валом редуктора и нагрузкой; M=c_мi– вращающий момент двигателя; М_н – момент нагрузки; с_е, с_м – константы.

Уравнения (2.1)-(2.2) полностью описывают процессы в ЭД, но не могут рассматриваться в качестве модели динамического звена, пока не выполнены сформулированные выше правила. Для перехода к уравнению динамического звена сначала подставим выражение для М в уравнение (2.2), выразим из него ток через выходной сигнал звена W и возмущающее воздействие М_н и подставим ток в уравнение (2.1):

,

.

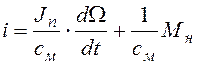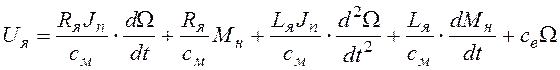Теперь сгруппируем выходной сигнал звена и его производные в левой части уравнения, входные сигналы – в правой части:

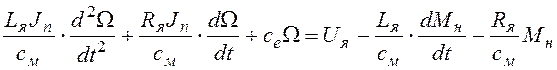
и для выполнения третьего требования разделим уравнение на с_е:

.

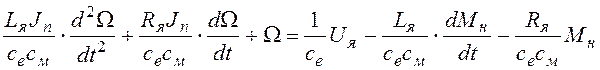Структура полученного уравнения отражает наличие у динамического звена тех или иных свойств. Величины коэффициентов – глубину этих свойств. Поэтому коэффициенты уравнений динамических звеньев имеют различный смысл, названия и обозначения. Коэффициенты при производных – постоянные времени, коэффициенты при входных сигналах в правой части – коэффициенты передачи. При введении постоянных времени следует заботиться об обеспечении одинаковой размерности у всех слагаемых в уравнении (первая производная имеет размерность с^-1, вторая – с^-2 и так далее; постоянная времени имеет размерность «с»). При появлении в уравнении производных более высокого порядка коэффициенты при них должны содержать произведения постоянных времени.

Перепишем полученное уравнение с использованием постоянных времени и коэффициентов передачи:

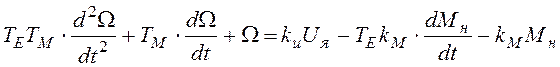,        (2.3)

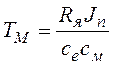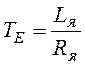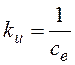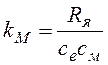где введены стандартные обозначения для параметров ЭД постоянного тока:  - электромеханическая постоянная времени;  -электрическая постоянная времени;  - коэффициент передачи по напряжению якоря;  - коэффициент передачи по моменту нагрузки.

Для перехода к передаточным функциям вспомним, что в соответствии с теоремой дифференцирования изображение по Лапласу производной оригинала x(t) связано с изображением X(s) самого оригинала следующим образом:

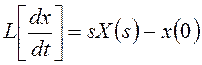, а при нулевых начальных условиях, что оговаривается в определении передаточной функци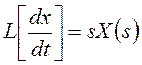и

 и .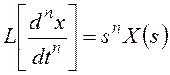

С учетом этого перейдем от (2.3) к операторному уравнению для изображений:

.

Операторное уравнение является алгебраическим и допускает следующее преобразование:

.

Теперь, поочередно пренебрегая одним из входных сигналов звена и деля уравнение на выражение в скобках в правой части, получим передаточные функции:

,

.

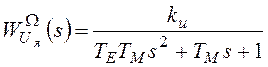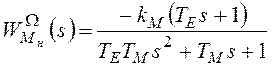Редуктор (Р) с учетом выбора входного и выходного сигналов оказывается интегрирующим звеном:

,

,

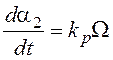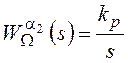, где 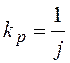 - коэффициент передачи, j– передаточное число редуктора.

Теперь можем составить структурно-динамическую схему системы (рисунок 18), на которой динамические свойства звеньев описываются передаточными функциями.