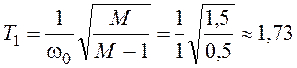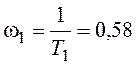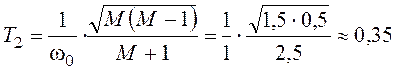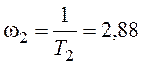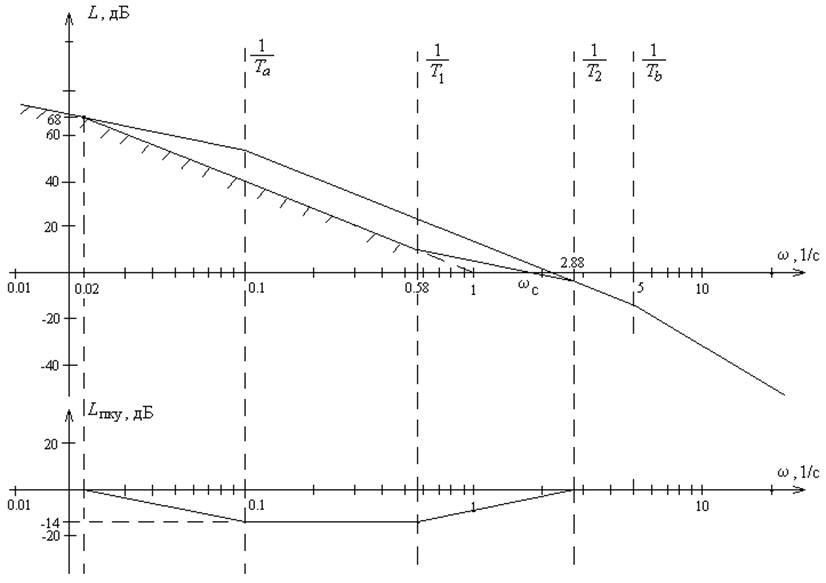
Синтез систем управления, страница 3

; ;

; .

Внизу на рисунке представлена асимптотическая ЛАХ последовательного корректирующего устройства, полученная по соотношению: . Соответствующая ей передаточная функция имеет вид: 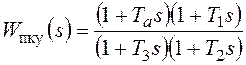, где .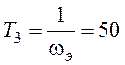

Передаточная функция разомкнутой синтезированной системы соответствует желаемой ЛАХ: 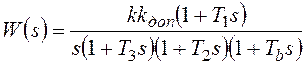. Определим для нее частоту среза  и запас устойчивости по фазе:

.

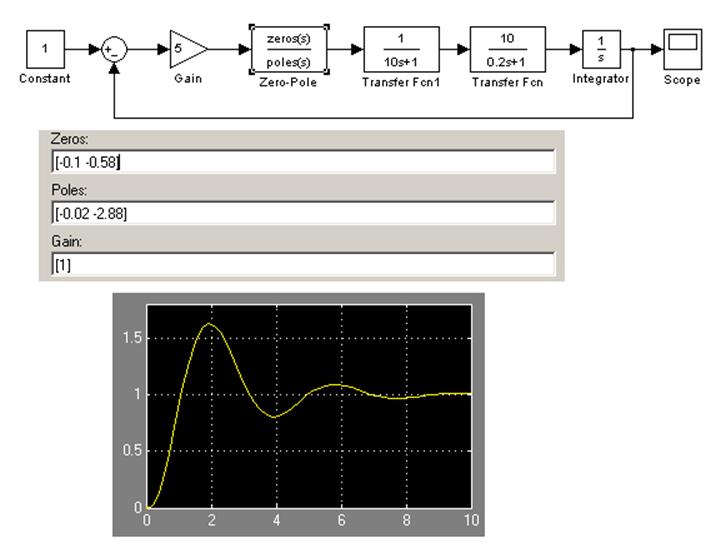
На рисунке представлены модель скорректированной системы в Simulink и ее переходная характеристика, демонстрирующая перерегулирование немногим более 60%.

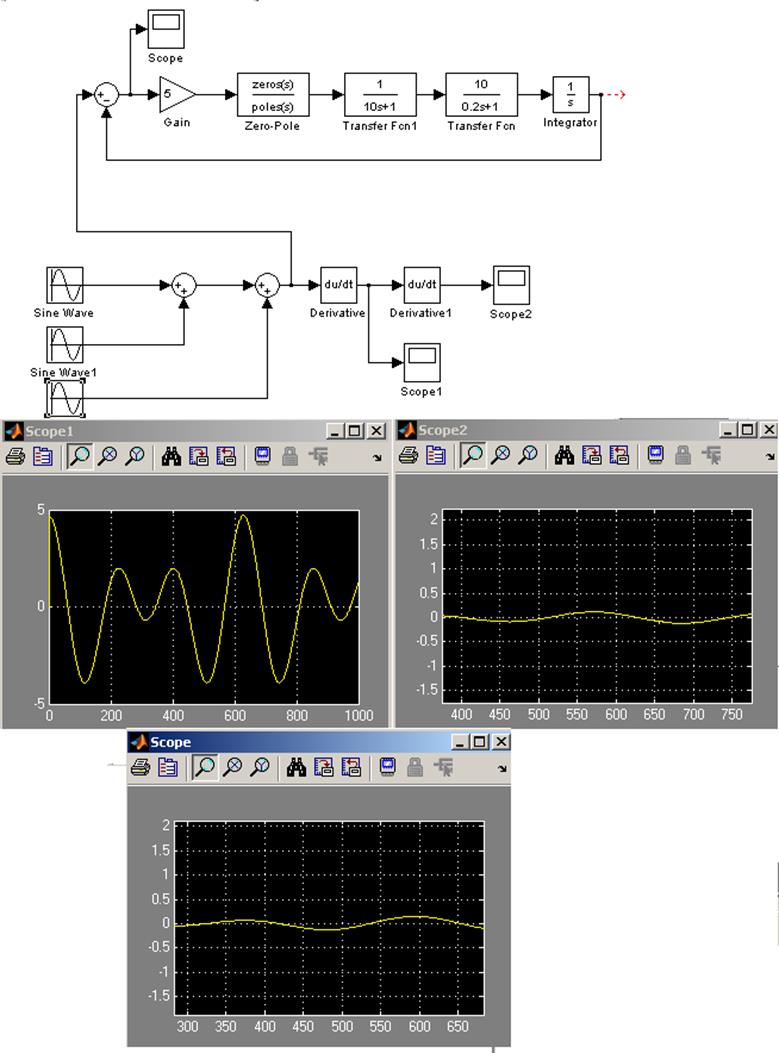
Для проверки выполнения требований к точности системы проведем моделирование с полигармоническим входным сигналом с заданным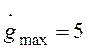и  и 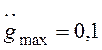 () и убедимся, что амплитуда сигнала ошибки не превышает заданной допустимой величины (рисунок).

Наиболее распространенные корректирующие звенья последовательного типа и их характеристики представлены в таблице 1.

Таблица 1

На практике далеко не всегда удается построить требуемое ПКУ или оно оказывается неоправданно сложным.

Непрерывные корректирующие звенья вводятся в состав системы тремя способами:

- последовательные корректирующие звенья (рисунок 17а);

- параллельные корректирующие звенья (рисунок 17б);

- гибкие отрицательные обратные связи (рисунок 17в).

Здесь  - звено, входящее в состав непрерывной части корректируемой системы.

Использование того или иного типа корректирующих звеньев определяется удобством технической реализации. В линейных системах для корректирующего устройства одного типа всегда можно подобрать эквивалентное, то есть обеспечивающее для данной системы аналогичные динамические свойства, корректирующее устройство второго или третьего типа. Расчетные соотношения для получения передаточных функций эквивалентных корректирующих звеньев в соответствии с рисунком 17 можно получить на основе следующего равенства:

.

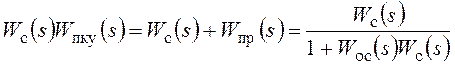В результате получаются следующие соотношения:

,  ,

,  ,

,  .

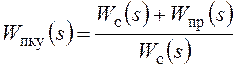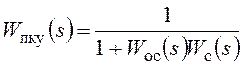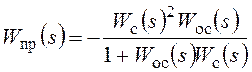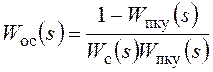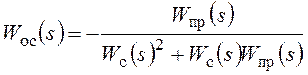Последовательные корректирующие звенья удобно применять, когда в системе используется электрический сигнал, величина которого функционально связана с сигналом ошибки, без введения высокочастотных модулированных сигналов. Тогда последовательные корректирующие звенья могут быть построены в виде достаточно простых схем из резисторов, конденсаторов и катушек индуктивности.

Параллельные корректирующие звенья удобны, когда необходимо реализовать сложный закон управления с введением интегралов и производных от сигнала ошибки.

Достоинством обратных связей является обеспечение дополнительного эффекта уменьшения влияния нелинейностей и нестабильности характеристик охватываемой части системы на работу системы в целом.