Алгебраический критерий устойчивости Гурвица

Лекция 11.Алгебраический критерий устойчивости Гурвица

Алгебраический критерий устойчивости Гурвица позволяет анализировать устойчивость замкнутой системы по ее характеристическому полиному D(s). Удобство применения критерия обусловлено тем, что вся процедура анализа сводится к работе с алгебраическими неравенствами, составляемыми из коэффициентов D(s) по простым правилам. Критерий также позволяет решать некоторые простые задачи оценки качества и синтеза систем. Примеры рассмотрены ниже.

Критерий Гурвица, как и другие критерии устойчивости, применяется, если для системы выполнено необходимое условие устойчивости (все коэффициенты D(s) положительны) и порядок системы n выше второго. Отметим здесь, что в частном случае, когда проверка необходимого условия устойчивости дала отрицательный результат из-за того, что один из коэффициентов оказался равным нулю при положительности остальных, система может находиться на границе устойчивости. Проверить это проще всего с помощью критерия Гурвица.

С повышением n удобство применения критерия Гурвица снижается в связи с усложнением получаемых неравенств. Поэтому на практике его применяют для систем не выше 5-6 порядка.

Пусть известен характеристический полином замкнутой системы: D(s)=a₀sⁿ+a₁s^n-1+…+a_n.

Критерий предусматривает работу с матрицей, составленной из коэффициентов полинома D(s) по следующим правилам:

- матрица квадратная размерностью ;

- главная диагональ заполняется коэффициентами, начиная с a₁ в порядке возрастания;

- в строки с нечетными номерами заносятся коэффициенты с нечетными номерами в порядке возрастания;

- в строки с четными номерами заносятся коэффициенты с четными номерами, начиная с a₀, в порядке возрастания;

- коэффициенты в строках располагают вблизи главной диагонали, остальные элементы матрицы принимают равными нулю:

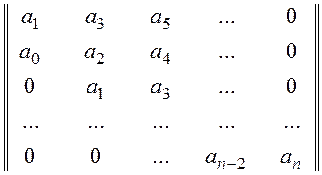.                                    (11.1)

При положительном коэффициенте a₀ для устойчивости системы достаточно, чтобы все определители Гурвица были положительны: D₁>0, D₂>0, ... , D_n>0.

Определители Гурвица – это угловые определители матрицы (11.1), получаемые по известным правилам:

,         ,       , …

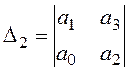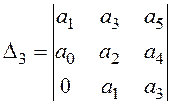Соответственно определитель D_n-1 получают, отбрасывая n-й столбец и  n-ю строку матрицы; определитель D_n соответствует всей матрице.

Отметим следующие свойства определителей Гурвица:

1. Если выполнено необходимое условие устойчивости, то всегда D₁>0.

2. При раскрытии D_n по последнему столбцу получим, D_n=a_nD_n-1, так как кроме a_n все элементы данного столбца равны нулю. Если выполнено необходимое условие устойчивости, то a_n>0. Следовательно, знак D_n совпадает со знаком D_n-1, и отдельно проверять его также не требуется.

В результате применение критерия Гурвица сводится к проверке n-2 неравенств, получаемых на основе определителей с D₂ по D_n-1.

Например, для системы третьего порядка требуется проверка одного неравенства:

D(s)=a₀s³+a₁s²+a₂s+a₃, .

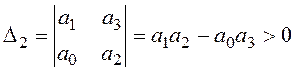Для системы четвертого порядка – двух неравенств:

D(s)=a₀s⁴+a₁s³+a₂s²+a₃s+a₄, ,

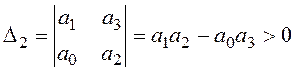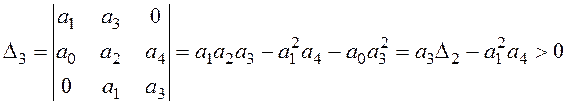
и так далее.

На основе критерия Гурвица могут быть обнаружены границы устойчивости. Признаком нахождения системы на границе устойчивости является равенство нулю последнего определителя (D_n=0). С учетом соотношения D_n=a_nD_n-1 это может быть вызвано равенством нулю любого из сомножителей. Доказано, что при a_n=0 имеет место апериодическая граница устойчивости, при D_n-1=0 - колебательная