Произвольно выбираем конъюнкции 1235 и 2456.
Оптимизированная
функция ![]()
Сформируем новое характеристическое подмножество из исходной функции, заменив на «*» наборы, реализуемые уже оптимизированными ПМФ (столбец 10).
Оптимизируем ПМФ ![]() и
и ![]()
![]()
Сформируем
R![]() из элементарных
конъюнкций третьего и второго рангов:
из элементарных
конъюнкций третьего и второго рангов:
|
j |
№ |
Конъюнкция |
Покрываемый набор из |
Количество покрываемых импликант |
Множество импликант |
|
3 |
1 |
123 |
1236 |
* |
- |
|
2 |
124 |
- |
1 |
+ |
|
|
3 |
126 |
1236 |
* |
- |
|
|
4 |
134 |
- |
1 |
+ |
|
|
5 |
145 |
- |
1 |
+ |
|
|
6 |
146 |
- |
1 |
+ |
|
|
7 |
235 |
- |
2 |
+ |
|
|
8 |
256 |
- |
2 |
+ |
|
|
9 |
345 |
3456 |
* |
- |
|
|
10 |
456 |
3456 |
* |
- |
|
|
2 |
1 |
12 |
125 |
* |
- |
|
2 |
13 |
135 |
* |
- |
|
|
3 |
15 |
125 |
* |
- |
|
|
4 |
16 |
136 |
* |
- |
|
|
5 |
23 |
234 |
* |
- |
|
|
6 |
24 |
234 |
* |
- |
|
|
7 |
25 |
125 |
* |
- |
|
|
8 |
26 |
1236 |
* |
- |
|
|
9 |
34 |
234 |
* |
- |
|
|
10 |
35 |
135 |
* |
- |
|
|
11 |
45 |
245 |
* |
- |
|
|
12 |
46 |
246 |
* |
- |
|
|
13 |
56 |
156 |
* |
- |
Определим
оптимальное покрытие первичной ДНФ P![]() элементами функции R
элементами функции R![]() :
:
|
1 2 4 |
1 3 4 |
1 4 5 |
1 4 6 |
1 2 5 6 |
1 3 5 6 |
2 3 4 5 |
2 3 4 6 |
2 3 5 6 |
|
|
124 |
|
||||||||
|
134 |
|
||||||||
|
145 |
|
||||||||
|
146 |
|
||||||||
|
235 |
|
|
|||||||
|
256 |
|
|
Существенными являются все конъюнкции, они будут включены в окончательное решение.
Оптимизированная
функция: ![]() .
.
![]()
Сформируем
R![]() из элементарных
конъюнкций второго ранга:
из элементарных
конъюнкций второго ранга:
|
j |
№ |
Конъюнкция |
Покрываемый набор из |
Количество покрываемых импликант |
Множество импликант |
|
2 |
1 |
15 |
- |
3 |
+ |
|
2 |
24 |
- |
3 |
+ |
Определим
оптимальное покрытие первичной ДНФ P![]() элементами функции R
элементами функции R![]() :
:
|
1 4 |
3 6 |
1 2 5 |
1 3 5 |
1 5 6 |
2 3 4 |
2 4 5 |
2 4 6 |
|
|
15 |
|
|
|
|||||
|
24 |
|
|
|
Существенными являются все конъюнкции, они будут включены в окончательное решение.
Оптимизированная
функция: ![]() .
.
Оптимизация
функции ![]() закончена.
Получено следующее представление:
закончена.
Получено следующее представление:
![]()

Декомпозиция системы ФАЛ методом ПМФ закончена. В результате декомпозиции получены следующие представления функций:
![]()
![]()
![]()
![]()
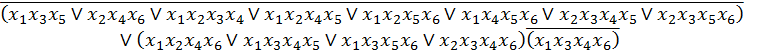
![]()

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.