Квантовые свойства кристаллов. Классификация кристаллов по электрической проводимости. Cверхпроводимость, страница 5

Посредством легирования на одном монокристалле можно создать целую электронную схему. Такие схемы называют интегральными. Главными преимуществами интегральных схем являются их малые размеры, обусловленная этим высокая скорость протекания процессов, малая потребляемая мощность, надёжность в эксплуатации. Для проектирования интегральных схем широко используются электронные вычислительные машины. Результаты соответствующих расчётных и конструкторских работ используются для создания шаблонов, с применением которых в определённой последовательности производятся технологические операции – травление, напыление, диффузия, итогом которых является интегральная схема как функциональный блок. 

Рассмотрим теперь некоторые свойства кристаллических твердых тел.

Одним из важных свойств твердого тела является его теплопроводность. В твердом теле существует два основных механизма переноса тепловой энергии: перенос энергии свободными электронами и перенос энергии тепловыми колебаниями атомов. Для диэлектриков, в которых отсутствуют свободные электроны, характерен перенос энергии тепловыми колебаниями атомов решетки (фононами). Теплопроводность этого типа является решеточной. В металлах действуют оба механизма одновременно, поэтому  коэффициент теплопроводности равен сумме решёточной К_реш и электронной К_э составляющих: К = К_э + К_реш, и при обычных температурах, как правило, К_э ≥ К_реш. В процессе теплопроводности каждый электрон при наличии градиента температуры переносит энергию kT, вследствие чего отношение электронной составляющей коэффициента теплопроводности К_э к электрической проводимости σ металла в широком интервале температур пропорционально температуре (закон Видемана – Франца):

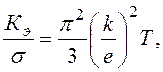
 где k — постоянная  Больцмана, е — модуль заряда электрона. Величина 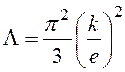 универсальная постоянная, называемая числом Лоренца и равная Λ = 2,45·10^-8 Вт·Ом·К^-2. Это значение удовлетворительно соответствует экспериментальным данным при комнатной температуре. В связи с тем, что у большинства металлов К_реш ≤ К_э, в законе Видемана — Франца можно с приемлемой точностью заменить К_э величиной К.

В квантовой теории металлов электрическую проводимость металла определяют по формуле

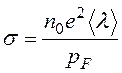, где  – импульс электрона, находящегося на уровне Ферми ;  не зависит от температуры;  – средняя длина свободного пробега электронов, находящихся на уровне Ферми.

Закон Видемана – Франца является следствием того, что теплопроводность металлов (как и их электропроводность) осуществляется свободными электронами.

Обнаруженные экспериментально отступления от закона Видемана – Франца обусловлены наличием неупругих столкновений электронов.

Средняя длина свободного пробега  фононов является кинетической характеристикой, аналогичной средней длине свободного пробега молекулы. Коэффициент решеточной теплопроводности кристаллов определяют по формуле

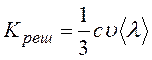, где с – теплоёмкость единицы объема вещества. Например, для решётки хлористого натрия при температуре 0⁰С и значениях Дж/(К·м³) и Дж/(м·К·с), средняя длина свободного пробега фононов м, что в 4 раза превышает расстояние между соседними ионами в кубической гранецентрированной решётке хлористого натрия м. Величина  определяется геометрическим рассеянием фононов (рассеяние на границах кристалла, дефектах решётки и аморфных структурах) и рассеянием фононов на ангармонических колебаниях узлов решётки (рассеяние фононов на фононах). Гармонические колебания причиной  рассеяния фононов не являются.

Рассеянием фононов на фононах при высоких температурах (T > T_D,  где T_D – температура Дебая [1]) обусловлена гиперболическая зависимость средней длины свободного пробега фононов от температуры: 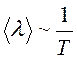. При    T << T_D  средняя длина свободного пробега зависит от температуры в соответствии с иным законом: 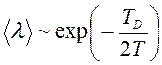. Геометрическое рассеяние существенно при больших значениях , сравнимых с линейными размерами d образца. В таких условиях, реализующихся при низких температурах, происходит резкое уменьшение теплопроводности чистых кристаллов, и выполняется соотношение 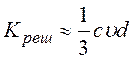. При не очень низких температурах  в соответствии с зависимостью 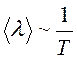. При низких температурах , так как (закон Дебая). В качестве примера на рисунке 24.3 приведена зависимость коэффициента теплопроводности меди от температуры в диапазоне 0 ≤ Т ≤ 100 К.