Квантовые свойства кристаллов. Классификация кристаллов по электрической проводимости. Cверхпроводимость, страница 11

Если сверхпроводник поместить во внешнее магнитное поле, то при достижении индукцией поля некоторого критического значения B_к сверхпроводник становится обычным проводником. Значение индукции B_к уменьшается при повышении температуры и становится равным нулю при критической температуре (рисунок 24.5).

С достаточной степенью точности зависимость B_к(T) можно представить в виде параболической функции:

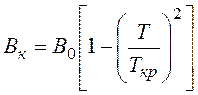, где B₀ – индукция критического поля при 0 К. Такая зависимость характерна для сверхпроводников первого рода (свинца, тантала, олова и др.), названных так  потому, что их фазовый переход в сверхпроводящее состояние – переход первого рода – их свободная энергия и теплоёмкость при достижении критической температуры изменяются скачком. Значение B₀ для чистых металлов достаточно мало и увеличивается при увеличении T_кр. При T_кр порядка 1 К значение B₀ – порядка сотых долей тесла; при больших значениях T_кр значение B₀ может достигать десятых долей тесла.

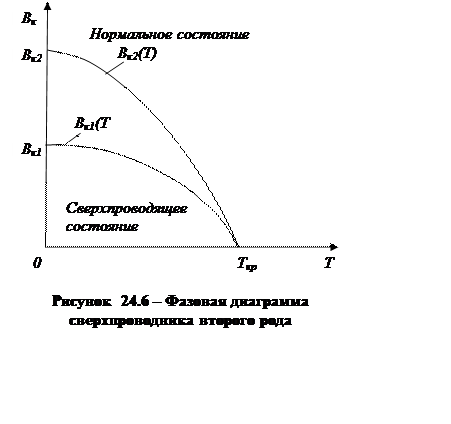
Для сверхпроводников второго рода (ниобий, Nb₃Sn и др.) зависимость фазового состояния от температуры и индукции внешнего магнитного поля более сложная. На рисунке 24.6 изображена фазовая диаграмма для цилиндрического образца из сверхпроводника второго рода. При  T < T_кр и     B > B_к2 вещество находится в нормальном состоянии. При B = B_к2 происходит фазовый переход из нормального состояния в смешанное, характеризующееся тем, что образец дробится на одновременно существующие небольшие области двух типов. В областях первого типа, обладающих обычной проводимостью, магнитное поле остаётся, а в областях второго типа магнитное поле исчезает, так как в них вещество переходит в сверхпроводящее состояние. Вследствие наличия областей второго типа образец становится сверхпроводящим.  Магнитное поле вытесняется из всего образца только при уменьшении значения индукции магнитного поля до       B = B_к1, когда полностью реализуется эффект Мейснера.

У сверхпроводников второго рода значения B_к2 во много раз превышают значения B_к, характерные для сверхпроводников первого рода. Поэтому сверхпроводники второго рода используют для изготовления сверхпроводящих соленоидов, посредством которых получают сильные магнитные поля.

Если индукция магнитного поля, обусловленного протекающим по сверхпроводнику электрическим током, достигает значения B_кр, сверхпроводимость исчезает. Плотность тока, при которой это происходит, называют критической плотностью тока.

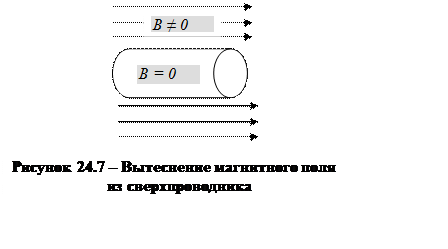
В 1933 году немецкие физики В. Мейснер и Р. Оксенфельд установили, что слабое магнитное поле не проникает вглубь сверхпроводника независимо от того, было ли поле включено до или после перехода в сверхпроводящее состояние (рисунок 24.7). В отличие от этого, в идеальном проводнике (то есть проводник с ничтожно малым сопротивлением) при уменьшении его удельного сопротивления индукция магнитного поля в объеме проводника не изменяется.

Эффект Мейснера объясняется экранирующим действием незатухающих токов, текущих в очень тонком поверхностном слое сверхпроводящего образца. Толщина этого слоя  характеризует также глубину проникновения в сверхпроводник внешнего магнитного поля.

Вытеснение магнитного поля из сверхпроводящего образца означает, что при наличии внешнего магнитного поля такой образец проявляет себя как идеальный диамагнетик той же формы с магнитной проницаемостью  и магнитной восприимчивостью .

Полное вытеснение магнитного поля из вещества характерно для сверхпроводников первого рода. Сверхпроводники второго рода проявляют частичный эффект Мейснера.