15. Производные высших порядков. Ряд Тейлора
Определение 1: Производной второго порядка называют
производную от производной. Аналогично, производной ![]() -го
порядка называют производную от производной
-го
порядка называют производную от производной ![]() -го
порядка. Пишут
-го
порядка. Пишут ![]() ,
,
![]() ,
, ![]() ,
, ![]() . (91)
. (91)
Пример 1: Найти третью производную от функции ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
Пример 2: Вычислить семнадцатую производную от функции ![]() в точке
в точке
![]() .
.
 ,
,
 ,
,
 ,
,
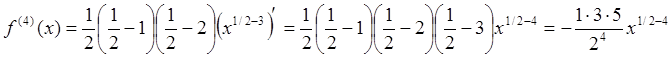 …
…
Нетрудно заметить, что выражение для производной ![]() -го порядка может быть записано в виде
-го порядка может быть записано в виде 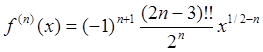 , откуда, подставляя
, откуда, подставляя ![]() , получаем
, получаем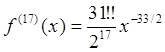 .
.
Наконец, положив ![]() , приходим к
окончательному результату
, приходим к
окончательному результату 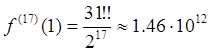 .
.
Определение 2: Дифференциалом ![]() - го порядка
называют величину
- го порядка
называют величину
![]() .
(92)
.
(92)
Как правило, вместо ![]() пишут
пишут ![]() (не путать с
(не путать с ![]() ),
откуда непосредственно следует одна из форм записи для
),
откуда непосредственно следует одна из форм записи для ![]() -й
производной:
-й
производной: ![]() .
.
Перейдем теперь к введению понятия ряда Тейлора. Для начала сформулируем три задачи, с которыми мы в той или иной степени уже встречались:
Задача 1: Вычислить с любой наперед заданной точностью (например 0.01) ![]() .
.
Отметим, что любой вычислительный алгоритм
базируется на четырех основных операциях (сложение, вычитание, умножение и
деление), которые могут быть реализованы, например, методом вычисления «в
столбик». Если при нахождении числа ![]() в качестве алгоритма
вычисления может быть предложен метод подбора:
в качестве алгоритма
вычисления может быть предложен метод подбора: ![]()
(![]()
![]() и т.д.), то при нахождении
и т.д.), то при нахождении ![]() четкий алгоритм
вычисления на первый взгляд отсутствует.
четкий алгоритм
вычисления на первый взгляд отсутствует.
Задача 2: Аппроксимировать функцию ![]() на интервале
на интервале ![]() полиномом
полиномом ![]() с любой
наперед заданной точностью.
с любой
наперед заданной точностью.
В предыдущем параграфе в качестве
наилучшей аппроксимации функции ![]() полиномом первой
степени (линейной функцией) вблизи центра интервала
полиномом первой
степени (линейной функцией) вблизи центра интервала ![]() была
предложена касательная
была
предложена касательная ![]() , однако на границе
интервала
, однако на границе
интервала ![]() и данная аппроксимация абсолютно не
применима. По-видимому, аппроксимация полиномом более высокой степени
и данная аппроксимация абсолютно не
применима. По-видимому, аппроксимация полиномом более высокой степени ![]() , содержащим
, содержащим ![]() подгоночный
параметр, позволит улучшить точность приближения на всем интервале.
подгоночный
параметр, позволит улучшить точность приближения на всем интервале.
Задача 3: Найти предел функции ![]() .
.
Все три перечисленных задачи могут быть успешно решены на основе формулы (ряда) Тейлора, отправной точкой для вывода которой является задача 2.
Определение 3: Функциональным рядом называют ряд, элементами
(слагаемыми) которого являются функции  , где
, где ![]() является, вообще говоря, комплексной
переменной.
является, вообще говоря, комплексной
переменной.
Определение 4: Степенным рядом называют функциональный ряд вида 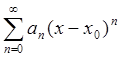 .
.
Предположим, что функция ![]() может
быть представлена в виде степенного ряда
может
быть представлена в виде степенного ряда
![]() , тогда
, тогда
![]() ,
, ![]() ,
, ![]() ,
, ![]() , …
, … ![]() ,
откуда получаем
,
откуда получаем 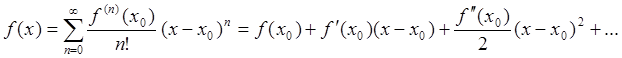 . (93)
. (93)
О представлении функции в виде ряда (93) говорят как о
разложении в ряд Тейлора в окрестности точки ![]() .
.
Приведем несколько формул, задающих разложение в
ряд Тейлора основных элементарных функций в окрестности точки ![]() :
:
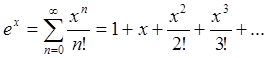 (94a)
(94a)
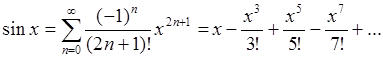 (94b)
(94b)
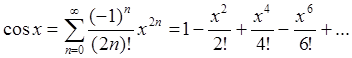 (94c)
(94c)
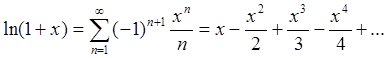 (94d)
(94d)
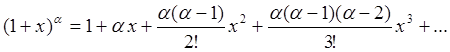 (94e)
(94e)
Формулы (94a,b) нам уже знакомы (смотри (59), (72)).
Пример 3: Используя общую формулу (93) получить разложение (94b).
Поскольку все производные четного порядка в точке ![]() равны нулю (
равны нулю (![]() ), а
значения нечетных производных вычисляются по формуле
), а
значения нечетных производных вычисляются по формуле ![]() ,
имеем
,
имеем 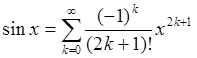 Ч.Т.Д.
Ч.Т.Д.
Отметим, что, как и следовало ожидать, разложение нечетной
функции ![]() производится только по нечетным степеням
переменной
производится только по нечетным степеням
переменной ![]() . В разложение четной функции
. В разложение четной функции ![]() , наоборот, входят только четные степени
переменной
, наоборот, входят только четные степени
переменной ![]() .
.
На рис. 22 показана аппроксимация функции ![]() полиномами 1, 3, 5 и 7 степени, полученными
на основании формулы (94b).
Как видно из рисунка, повышение степени полинома влечет за собой увеличение
точности аппроксимации на всем интервале
полиномами 1, 3, 5 и 7 степени, полученными
на основании формулы (94b).
Как видно из рисунка, повышение степени полинома влечет за собой увеличение
точности аппроксимации на всем интервале ![]() . При
аппроксимации полиномом седьмой степени погрешность (максимальная на краях интервала)
не превосходит 10% (решение задачи 2).
. При
аппроксимации полиномом седьмой степени погрешность (максимальная на краях интервала)
не превосходит 10% (решение задачи 2).
В параграфе 13 было показано, что разложение (94b) позволяет без труда найти предел ![]() (решение задачи 3).
(решение задачи 3).
Пример 4: Используя общую формулу (93) получить разложение (94d).
Поскольку 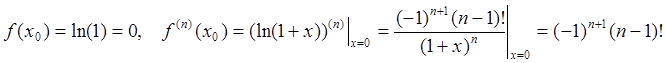 , получаем
, получаем  Ч.Т.Д.
Ч.Т.Д.
Отметим, что в формулах (94d,e) натуральный логарифм и
степенная функция раскладываются в ряд Тейлора в окрестности аргумента, равного
единице (![]() ).
).
Разложение данных функций в окрестности нуля невозможно,
поскольку ![]() не определен в точке
не определен в точке ![]() , а для степенной функции
, а для степенной функции ![]() с показателем
с показателем ![]() при
при ![]() по крайней мере не определены все
производные. С другой стороны, при аргументе
по крайней мере не определены все
производные. С другой стороны, при аргументе ![]() , как
функции, так и все их производные легко вычисляются.
, как
функции, так и все их производные легко вычисляются.
Пример 5: Используя формулы (94d,e), вычислить ![]() и
и ![]() с точностью 0.01.
с точностью 0.01.
Полагая ![]() ,
, ![]() , получаем:
, получаем:
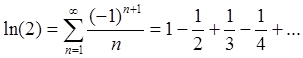 (смотри (57)). Как было показано,
согласно теореме Лейбница, последовательность частичных сумм сходится:
(смотри (57)). Как было показано,
согласно теореме Лейбница, последовательность частичных сумм сходится:
![]()
![]() .
.
Перейдем к вычислению ![]() .
.
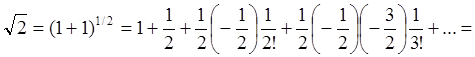
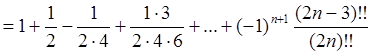 (смотри (4)).
(смотри (4)).
Сходимость ряда вновь следует из теоремы Лейбница:
знакочередующийся ряд, 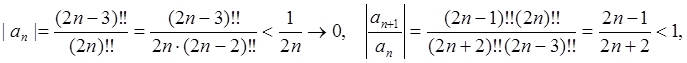
![]() , причем в данном случае последовательность
частичных сумм сходится быстрее:
, причем в данном случае последовательность
частичных сумм сходится быстрее:
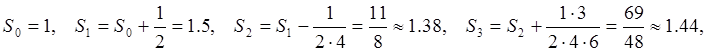
 (решение задачи 1).
(решение задачи 1).
Пример 6: Используя общую формулу (93), разложить полином ![]() в
ряд Тейлора в окрестности точек
в
ряд Тейлора в окрестности точек ![]() и
и ![]() .
.
Поскольку ![]() остальные
остальные ![]() , получаем:
, получаем:
при ![]() :
: ![]() , при
, при ![]() :
: ![]() .
.
Как и следовало ожидать, аппроксимация полинома третьей
степени полиномом той же самой (третьей) степени является точной (используя
формулу бинома Ньютона (27) легко показать, что обе аппроксимации совпадают при
всех ![]() ). В то же время, в окрестности точки
). В то же время, в окрестности точки ![]() (например, когда
(например, когда ![]() )
можно упростить исходную функцию, заменив ее с высокой точностью линейной
)
можно упростить исходную функцию, заменив ее с высокой точностью линейной ![]() (смотри рис. 23). В окрестности точки
(смотри рис. 23). В окрестности точки ![]() (например, когда
(например, когда ![]() )
исходная функция может быть аппроксимирована параболой
)
исходная функция может быть аппроксимирована параболой ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.