2)
Возможно
вычисление пределов при ![]() .
.
Пример 7: Найти предел 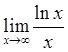 .
.
Условия Т2 выполняются: 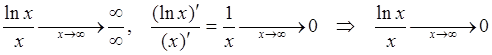 .
.
Пример 8: Найти предел ![]() .
.
В данном примере мы имеем дело с неопределенностью типа ![]() , которая также может быть раскрыта по
правилу Лопиталя:
, которая также может быть раскрыта по
правилу Лопиталя:
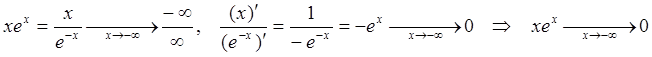 .
.
Пример 9: Найти предел ![]() .
.
Если в подкоренных выражениях пренебречь слагаемыми ![]() по сравнению с
по сравнению с ![]() , мы
приходим к неверному результату:
, мы
приходим к неверному результату: ![]() . Данное обстоятельство обусловлено тем, что старший член
разложения (пропорциональный
. Данное обстоятельство обусловлено тем, что старший член
разложения (пропорциональный ![]() ) для всей функции в
целом отсутствует, что делает пренебрежение слагаемыми
) для всей функции в
целом отсутствует, что делает пренебрежение слагаемыми ![]() незаконным.
Более точное рассмотрение дает:
незаконным.
Более точное рассмотрение дает: ![]() при
при ![]()
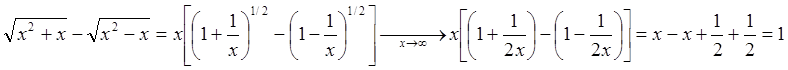 .
.
17. Сходимость ряда Тейлора. Ряд Лорана
Как отмечалось в предыдущем параграфе, существование функции
и всех ее производных в точке ![]() позволяет написать ряд
Тейлора для данной функции в окрестности точки
позволяет написать ряд
Тейлора для данной функции в окрестности точки ![]() . Однако
для того, чтобы можно было говорить о разложении функции в ряд Тейлора
при некотором
. Однако
для того, чтобы можно было говорить о разложении функции в ряд Тейлора
при некотором ![]() (чтобы можно было поставить знак
равенства между функцией и соответствующим рядом
(чтобы можно было поставить знак
равенства между функцией и соответствующим рядом 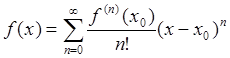 ),
необходимо, чтобы полученный ряд сходился при данном
),
необходимо, чтобы полученный ряд сходился при данном ![]() .
Оказывается, что в большинстве случаев сходимость ряда Тейлора имеет место не
при всех
.
Оказывается, что в большинстве случаев сходимость ряда Тейлора имеет место не
при всех ![]() , а только в некоторой окрестности точки
, а только в некоторой окрестности точки ![]() .
.
Определение 1: Множество всех ![]() , при которых
функциональный ряд
, при которых
функциональный ряд ![]() сходится, называют областью
сходимости ряда.
сходится, называют областью
сходимости ряда.
Пример 1: Исследовать сходимость ряда Тейлора для функции ![]() в
окрестности точки
в
окрестности точки ![]() .
.
В отличие от точки ![]() , в которой функция (и
все ее производные) не определены, точка
, в которой функция (и
все ее производные) не определены, точка ![]() позволяет
написать ряд Тейлора:
позволяет
написать ряд Тейлора:
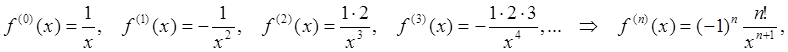

Данный ряд представляет собой геометрическую прогрессию с
первым (нулевым) членом ![]() и знаменателем
и знаменателем ![]() . Как было показано в параграфе 10 (смотри
(54)), ряд, составленный из членов геометрической прогрессии, сходится при
. Как было показано в параграфе 10 (смотри
(54)), ряд, составленный из членов геометрической прогрессии, сходится при ![]() к величине
к величине 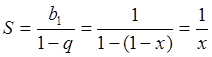 и
расходится при
и
расходится при ![]() . Что касается границ интервала
. Что касается границ интервала ![]() , то дополнительное рассмотрение
показывает:
, то дополнительное рассмотрение
показывает:
при ![]() :
: 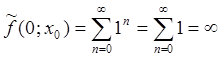 (сумма
ряда равна бесконечности, также как и предел функции изнутри области сходимости
(сумма
ряда равна бесконечности, также как и предел функции изнутри области сходимости
![]() );
);
при ![]() :
: 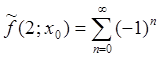 (ряд
расходится, в то время как значение функции равно
(ряд
расходится, в то время как значение функции равно ![]() ). Таким
образом, ряд сходится на интервале
). Таким
образом, ряд сходится на интервале ![]() , симметричном
относительно точки
, симметричном
относительно точки ![]() .
.
Теорема 1: Если степенной ряд сходится при некотором ![]() , то он сходится (причем абсолютно) и при
любом
, то он сходится (причем абсолютно) и при
любом ![]() . Наоборот, если степенной ряд расходится
при некотором
. Наоборот, если степенной ряд расходится
при некотором ![]() , то он расходится и при любом
, то он расходится и при любом ![]() .
.
Действительно, для начала отметим, что из сходимости ряда ![]() следует ограниченность последовательности
следует ограниченность последовательности ![]() (
(![]() начиная с некоторого
начиная с некоторого ![]() все
все ![]() , следовательно
для любого
, следовательно
для любого ![]() выполняется ограничение
выполняется ограничение ![]() ). Далее, пусть ряд сходится в некоторой
точке
). Далее, пусть ряд сходится в некоторой
точке ![]() , тогда
, тогда ![]() , причем для любого
, причем для любого ![]() выполняется неравенство
выполняется неравенство  , следовательно
, следовательно
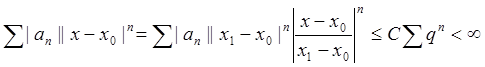 . Первая часть теоремы
доказана.
. Первая часть теоремы
доказана.
Расходимость ряда при любых ![]() доказывается
от противного. Действительно, если ряд сходится при
доказывается
от противного. Действительно, если ряд сходится при ![]() , то
согласно первой части теоремы он сходится и при
, то
согласно первой части теоремы он сходится и при ![]() , что
противоречит условию. Ч.Т.Д.
, что
противоречит условию. Ч.Т.Д.
Приведенное доказательство полностью справедливо
и при рассмотрении комплексных рядов (![]() -
комплексные числа). Таким образом, степенной ряд
-
комплексные числа). Таким образом, степенной ряд ![]() сходится
абсолютно внутри некоторого круга (на комплексной плоскости) с центром в
точке
сходится
абсолютно внутри некоторого круга (на комплексной плоскости) с центром в
точке ![]() и радиусом
и радиусом ![]() и
расходится вне этого круга. На границе круга степенной ряд может как сходиться,
так и расходиться.
и
расходится вне этого круга. На границе круга степенной ряд может как сходиться,
так и расходиться.
Определение 2: Радиус ![]() называют радиусом
сходимости степенного ряда.
называют радиусом
сходимости степенного ряда.
Радиус сходимости может быть найден по одной из следующих формул:
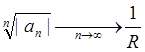 (Коши),
(Коши), 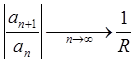 (Даламбер),
(96)
(Даламбер),
(96)
которые непосредственно вытекают из признаков сходимости Коши и Даламбера (смотри параграф 10).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.