16. Раскрытие неопределенностей
Ряд Тейлора часто используется для раскрытия
неопределенностей, возникающих при вычислении пределов. Рассмотрим предел
отношения функций ![]() . Если в точке
. Если в точке ![]() определены обе функции и их производные,
то, разложив числитель и знаменатель по формуле (93) в окрестности точки
определены обе функции и их производные,
то, разложив числитель и знаменатель по формуле (93) в окрестности точки ![]() , получаем
, получаем
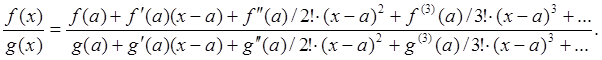
Отметим, что при ![]() каждое последующее
слагаемое в разложении является величиной более высокого порядка малости, по
сравнению с предыдущим, в том случае, если соответствующая производная отлична
от нуля. Данное обстоятельство позволяет сформулировать следующую теорему.
каждое последующее
слагаемое в разложении является величиной более высокого порядка малости, по
сравнению с предыдущим, в том случае, если соответствующая производная отлична
от нуля. Данное обстоятельство позволяет сформулировать следующую теорему.
Теорема 1: Если в окрестности точки ![]() функции
функции
![]() и
и ![]() могут
быть разложены в ряд Тейлора, то при вычислении предела
могут
быть разложены в ряд Тейлора, то при вычислении предела ![]() ,
как в числителе, так и в знаменателе следует оставлять только первое
отличное от нуля слагаемое разложения (слагаемое с первой не равной нулю
производной).
,
как в числителе, так и в знаменателе следует оставлять только первое
отличное от нуля слагаемое разложения (слагаемое с первой не равной нулю
производной).
Данное правило можно сформулировать и для более общего случая.
Теорема 2 (правило Лопиталя): Если ![]()
![]() , кроме того, существует конечный или
бесконечный предел
, кроме того, существует конечный или
бесконечный предел 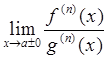 , то
, то 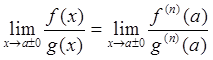 , (95)
, (95)
где ![]() есть любое конечное число или
символ
есть любое конечное число или
символ ![]() .
.
На практике Т2 используется следующим образом.
Если неопределенность типа ![]() или
или ![]() , возникающая при вычислении предела
, возникающая при вычислении предела 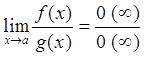 не может быть раскрыта непосредственно, то
рассматривают предел
не может быть раскрыта непосредственно, то
рассматривают предел 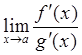 . Если при рассмотрении данного
предела вновь возникает неопределенность того же типа, которую вновь не удается
раскрыть непосредственно, то переходят к рассмотрению предела
. Если при рассмотрении данного
предела вновь возникает неопределенность того же типа, которую вновь не удается
раскрыть непосредственно, то переходят к рассмотрению предела 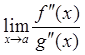 и так далее.
и так далее.
Как правило, использование Т1 и формул (94) позволяет раскрыть возникающую неопределенность быстрее, однако, в ряде случаев, использование Т2 оказывается более предпочтительным.
Пример 1: Вычислить предел 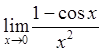 .
.
В данном случае мы имеем дело с неопределенностью типа ![]() .
.
1-й способ (Т1): Разлагая ![]() в ряд
Тейлора в окрестности точки
в ряд
Тейлора в окрестности точки ![]() по формуле (94c), получаем
по формуле (94c), получаем 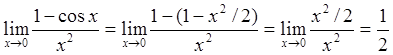 . Отметим, что как нулевой, так и первый член разложения
числителя и знаменателя в ряд Тейлора отсутствуют (функции и их производные в
точке
. Отметим, что как нулевой, так и первый член разложения
числителя и знаменателя в ряд Тейлора отсутствуют (функции и их производные в
точке ![]() равны нулю). Первое отличное от нуля
слагаемое является квадратичным.
равны нулю). Первое отличное от нуля
слагаемое является квадратичным.
2-й способ (Т2): ![]()
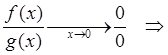 рассмотрим
рассмотрим 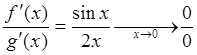 . Если вспомнить, что
. Если вспомнить, что 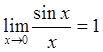 , то ответ становится очевидным на данном
этапе, в противном случае продолжаем:
, то ответ становится очевидным на данном
этапе, в противном случае продолжаем: 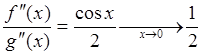 . В
данном примере, для раскрытия неопределенности по правилу Лопиталя нам пришлось
вычислять вторые производные. Это, как и следовало ожидать, находится в
соответствии с тем, что первые отличные от нуля слагаемые при разложении числителя
и знаменателя в ряд Тейлора являются квадратичными.
. В
данном примере, для раскрытия неопределенности по правилу Лопиталя нам пришлось
вычислять вторые производные. Это, как и следовало ожидать, находится в
соответствии с тем, что первые отличные от нуля слагаемые при разложении числителя
и знаменателя в ряд Тейлора являются квадратичными.
Пример 2: Вычислить предел 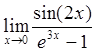 .
.
1-й способ: Поскольку при ![]() :
: ![]() , получаем
, получаем
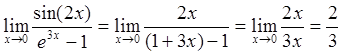 . Здесь первые отличные от нуля
слагаемые, как в числителе, так и в знаменателе, являются линейным.
. Здесь первые отличные от нуля
слагаемые, как в числителе, так и в знаменателе, являются линейным.
2-й способ: 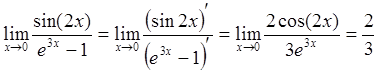 .
.
Пример 3: Вычислить предел 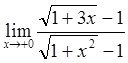 .
.
1-й способ: Согласно формуле (94e), при ![]() имеем:
имеем: ![]() . Полагая в числителе
. Полагая в числителе ![]() , а в знаменателе
, а в знаменателе ![]() ,
получаем
,
получаем
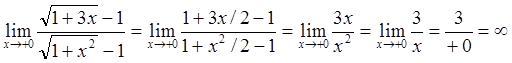 . В данном случае первое отличное
от нуля слагаемое в числителе – линейное, а в знаменателе – квадратичное.
. В данном случае первое отличное
от нуля слагаемое в числителе – линейное, а в знаменателе – квадратичное.
2-й способ: 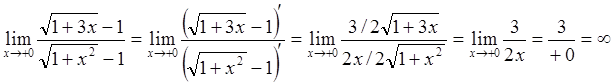 .
.
Пример 4: Вычислить предел 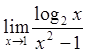 .
.
1-й способ: Поскольку при ![]() :
: ![]() , полагая
, полагая ![]() ,
имеем:
,
имеем: 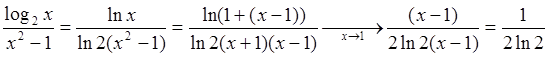 .
.
2-й способ: 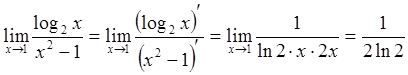 .
.
Пример 5: Вычислить предел 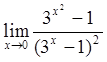 .
.
1-й способ: Поскольку ![]() (при
(при ![]() ), имеем:
), имеем:
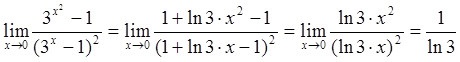 .
.
2-й способ:
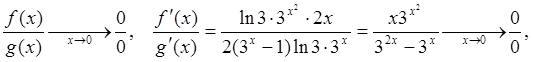
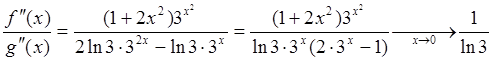 .
.
Обобщение Т2 по сравнению с Т1 состоит в следующем:
1)
Некоторые
производные могут быть не определены в точке ![]() . В этом
случае достаточно существования односторонних пределов (справа или слева).
. В этом
случае достаточно существования односторонних пределов (справа или слева).
Пример 6: Найти предел 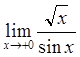 .
.
Функция ![]() не может быть разложена
в ряд Тейлора в окрестности нуля, тем не менее, условия Т2 выполняются:
не может быть разложена
в ряд Тейлора в окрестности нуля, тем не менее, условия Т2 выполняются: ![]()
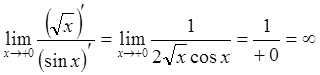 ,
следовательно
,
следовательно 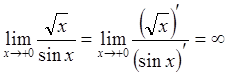 . Отметим, что в данном случае
можно воспользоваться и Т1:
. Отметим, что в данном случае
можно воспользоваться и Т1: 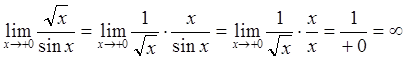 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.