Математический анализ функции одной переменной: Учебное пособие. Часть 2 (Производные высших порядков. Ряд Тейлора. Раскрытие неопределенностей. Сходимость ряда Тейлора. Ряд Лорана)

15. Производные высших порядков. Ряд Тейлора

Определение 1: Производной второго порядка называют производную от производной. Аналогично, производной -го порядка называют производную от производной -го порядка. Пишут ,

,  ,  .     (91)

Пример 1: Найти третью производную от функции .

,   ,   .

Пример 2: Вычислить семнадцатую производную от функции  в точке .

,   

,

,    

…

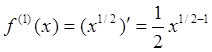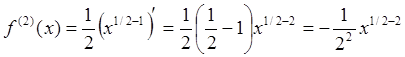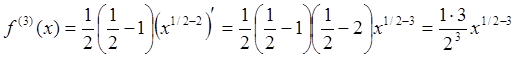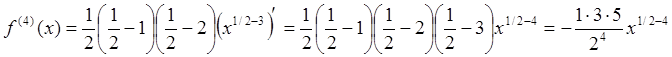Нетрудно заметить, что выражение для производной -го порядка может быть записано в виде 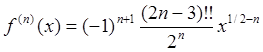, откуда, подставляя , получаем.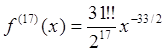

Наконец, положив , приходим к окончательному результату .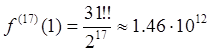

Определение 2: Дифференциалом - го порядка называют величину

.                                                         (92)

Как правило, вместо  пишут  (не путать с ), откуда непосредственно следует одна из форм записи для  -й производной: .

Перейдем теперь к введению понятия ряда Тейлора. Для начала сформулируем три задачи, с которыми мы в той или иной степени уже встречались:

Задача 1: Вычислить с любой наперед заданной точностью (например 0.01)  .

Отметим, что любой вычислительный алгоритм базируется на четырех основных операциях (сложение, вычитание, умножение и деление), которые могут быть реализованы, например, методом вычисления «в столбик». Если при нахождении числа  в качестве алгоритма вычисления может быть предложен метод подбора:

(

 и т.д.), то при нахождении  четкий алгоритм вычисления на первый взгляд отсутствует.

Задача 2: Аппроксимировать функцию  на интервале  полиномом  с любой наперед заданной точностью.

В предыдущем параграфе в качестве наилучшей аппроксимации функции  полиномом первой степени (линейной функцией) вблизи центра интервала  была предложена касательная , однако на границе интервала  и данная аппроксимация абсолютно не применима. По-видимому, аппроксимация полиномом более высокой степени , содержащим  подгоночный параметр, позволит улучшить точность приближения на всем интервале.

Задача 3: Найти предел функции .

Все три перечисленных задачи могут быть успешно решены на основе формулы (ряда) Тейлора, отправной точкой для вывода которой является задача 2.

Определение 3: Функциональным рядом называют ряд, элементами (слагаемыми) которого являются функции 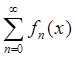, где  является, вообще говоря, комплексной переменной.

Определение 4: Степенным рядом называют функциональный ряд вида .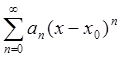

Предположим, что функция  может быть представлена в виде степенного ряда

, тогда

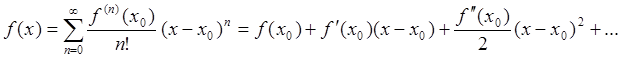,  ,  ,  , … , откуда получаем    .             (93)

О представлении функции в виде ряда (93) говорят как о разложении в ряд Тейлора в окрестности точки .

Приведем несколько формул, задающих разложение в ряд Тейлора основных элементарных функций в окрестности точки :

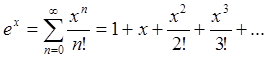                                                               (94a)

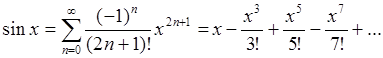                                        (94b)

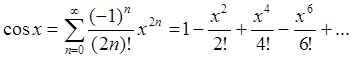                                               (94c)

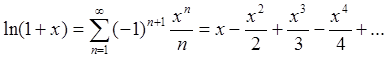                                         (94d)

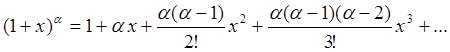                                (94e)

Формулы (94a,b) нам уже знакомы (смотри (59), (72)).

Пример 3: Используя общую формулу (93) получить разложение (94b).

Поскольку все производные четного порядка в точке  равны нулю (), а значения нечетных производных вычисляются по формуле , имеем 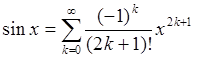  Ч.Т.Д.

Отметим, что, как и следовало ожидать, разложение нечетной функции  производится только по нечетным степеням переменной . В разложение четной функции , наоборот, входят только четные степени переменной .

На рис. 22 показана аппроксимация функции  полиномами 1, 3, 5 и 7 степени, полученными на основании формулы (94b). Как видно из рисунка, повышение степени полинома влечет за собой увеличение точности аппроксимации на всем интервале . При аппроксимации полиномом седьмой степени погрешность (максимальная на краях интервала) не превосходит 10% (решение задачи 2).

В параграфе 13 было показано, что разложение (94b) позволяет без труда найти предел  (решение задачи 3).

Пример 4: Используя общую формулу (93) получить разложение (94d).

Поскольку 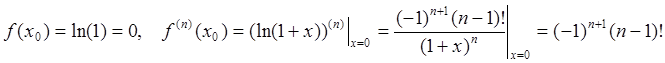,    получаем  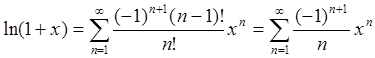   Ч.Т.Д.

Отметим, что в формулах (94d,e) натуральный логарифм и степенная функция раскладываются в ряд Тейлора в окрестности аргумента, равного единице ().

Разложение данных функций в окрестности нуля невозможно, поскольку  не определен в точке , а для степенной функции  с показателем  при  по крайней мере не определены все производные. С другой стороны, при аргументе , как функции, так и все их производные легко вычисляются.

Пример 5: Используя формулы (94d,e), вычислить  и  с точностью 0.01.

Полагая , , получаем:

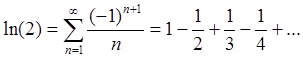   (смотри (57)). Как было показано, согласно теореме Лейбница, последовательность частичных сумм сходится:

.

Перейдем к вычислению .

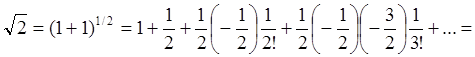
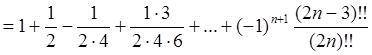     (смотри (4)).

Сходимость ряда вновь следует из теоремы Лейбница: знакочередующийся ряд, 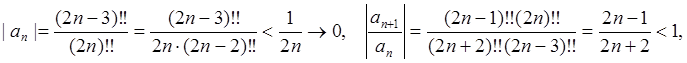  , причем в данном случае последовательность частичных сумм сходится быстрее:

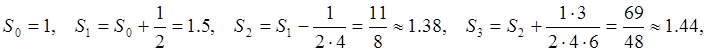
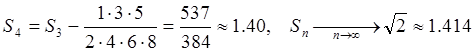     (решение задачи 1).

Пример 6: Используя общую формулу (93), разложить полином  в ряд Тейлора в окрестности точек  и .

Поскольку  остальные , получаем:

при :   , при :   .

Как и следовало ожидать, аппроксимация полинома третьей степени полиномом той же самой (третьей) степени является точной (используя формулу бинома Ньютона (27) легко показать, что обе аппроксимации совпадают при всех ). В то же время, в окрестности точки  (например, когда ) можно упростить исходную функцию, заменив ее с высокой точностью линейной  (смотри рис. 23). В окрестности точки  (например, когда ) исходная функция может быть аппроксимирована параболой .