







Тема:ПРИНЯТИЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Математическая модель
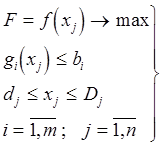 (1)
(1)
Три составляющие модели
1) Целевая функция (ЦФ)
ЦФ определяет, в каком смысле решение должно быть оптимальным.
В целевой функции возможны следующие действия:
¨ максимизация ( max ),
¨ минимизация ( min ),
¨ назначение заданного значения ( const ).
2) Ограничения (ОГР ) устанавливают зависимости между переменными:
![]()
В ограничениях могут использоваться следующие операторы сравнения:
<=, >=, =
3) Граничные условия (ГРУ) показывают, в каких пределах могут изменяться значения искомых переменных.
Классификация задач оптимизации
|
Исходные данные |
Искомые переменные |
Зависимости |
Классы задач |
|
Детерминированные |
Непрерывные |
Линейные |
Линейное программирование |
|
Детерминированные |
Целочисленные |
Линейные |
Целочисленное программирование |
|
Детерминированные |
Непрерывные, целочисленные |
Нелинейные |
Нелинейное программирование |
|
Случайные |
Непрерывные |
Линейные |
Стохастическое программирование |
Рис. 1
Задача линейного программирования. Математическая модель
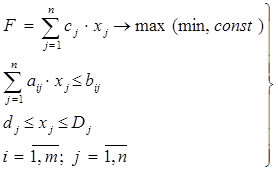 (2)
(2)
Методы решения задач линейного программирования
¨ графические
¨ аналитические
Решение задачи линейного программирования на примере задачи распределения ресурсов
Постановка задачи
Требуется определить оптимальный план выпуска продукции двух типов, при котором получаемая прибыль будет максимальна. Для изготовления продукции используются ресурсы трех видов, запасы которых ограничены.
|
Продукция 1 |
Продукция 2 |
Знак |
Наличие ресурсов |
|
|
Прибыль |
50 |
40 |
max |
|
|
Ресурс 1 |
2 |
5 |
<= |
20 |
|
Ресурс 2 |
8 |
5 |
<= |
40 |
|
Ресурс 3 |
5 |
6 |
<= |
30 |
Рис. 2
Математическая модель
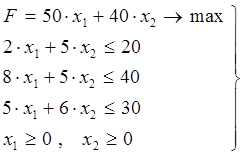 (3)
(3)
где:
xj – количество выпускаемой
продукции j-го типа, ![]()
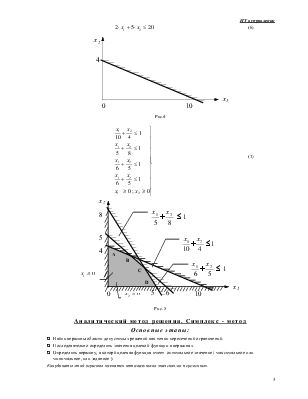
Графический метод решения
![]() (4)
(4)
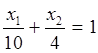 (5)
(5)
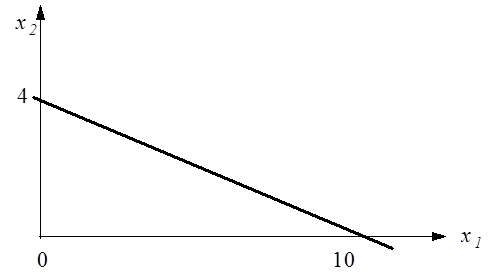
Рис. 3
![]() (6)
(6)
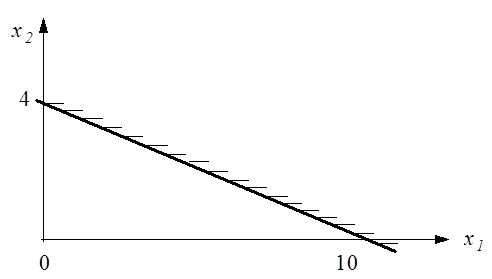
Рис.4
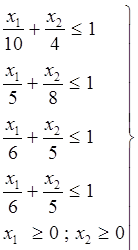 (7)
(7)
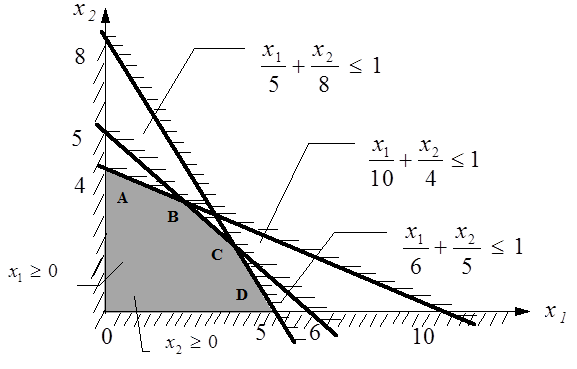
Рис. 5
Аналитический метод решения. Симплекс - метод
Основные этапы:
q Найти вершины области допустимых решений как точки пересечений ограничений.
q Последовательно определить значения целевой функции в вершинах.
q Определить вершину, в которй целевая функция имеет оптимальное значение ( максимальное или минимальное, или заданное ).
Координаты этой вершины являются оптимальными значениями переменных.
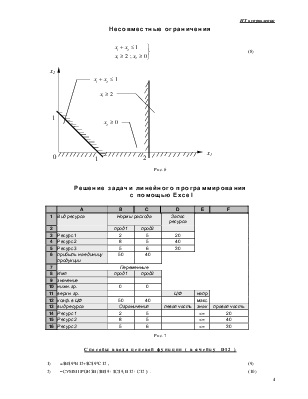
Несовместные ограничения
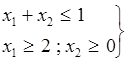 (8)
(8)
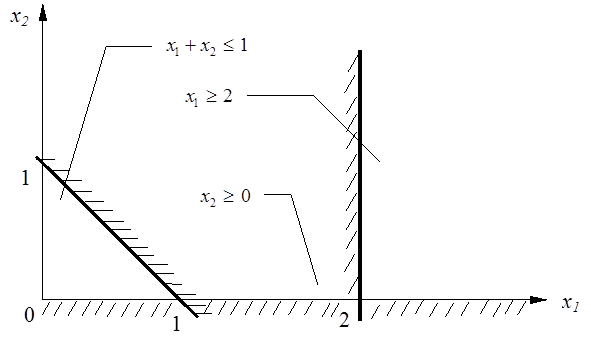 |
Решение задачи линейного программирования с помощью Excel
|
A |
B |
C |
D |
E |
F |
||||||
|
1 |
Вид ресурса |
Нормы расхода |
Запас ресурса |
||||||||
|
2 |
прод1 |
прод2 |
|||||||||
|
3 |
Ресурс 1 |
2 |
5 |
20 |
|||||||
|
4 |
Ресурс 2 |
8 |
5 |
40 |
|||||||
|
5 |
Ресурс 3 |
5 |
6 |
30 |
|||||||
|
6 |
прибыль на единицу продукции |
50 |
40 |
||||||||
|
7 |
Переменные |
||||||||||
|
8 |
Имя |
прод1 |
прод2 |
||||||||
|
9 |
значение |
||||||||||
|
10 |
нижн. гр. |
0 |
0 |
||||||||
|
11 |
верхн. гр. |
ЦФ |
напр |
||||||||
|
12 |
коэф. в ЦФ |
50 |
40 |
макс |
|||||||
|
13 |
вид ресурса |
Ограничения |
левая часть |
знак |
правая часть |
||||||
|
14 |
Ресурс 1 |
2 |
5 |
<= |
20 |
||||||
|
15 |
Ресурс 2 |
8 |
5 |
<= |
40 |
||||||
|
16 |
Ресурс 3 |
5 |
6 |
<= |
30 |
||||||
Рис. 7
Способы ввода целевой функции ( в ячейку D12 )
1) =$B$9*B12+$C$9*C12 , (9)
2) =СУММПРОИЗВ ($B$9 : $C$9, B12 : C12 ) . (10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.