Принятие оптимальных решений. Методы решения задач линейного программирования, страница 5

Корректировка таблицы для ввода условий задачи

Рис. 24

Формулы, содержащиеся в ячейках

Рис. 25

Далее надо выбрать команду Сервис – Поиск решения. На экране появится  соответствующее диалоговое окно ( рис. 26 ).

Параметры, которые требуется ввести в окно Поиск решения

1)  Установить целевую ячейку  – G10, равной минимальному значению

2)  Изменяемые  ячейки – B9:F9

3)  Ограничения: B9=7, C9>=C10, D9>=D10, E9>=E10, F9>=F10, G14=I14, G15=I15, G16=I16

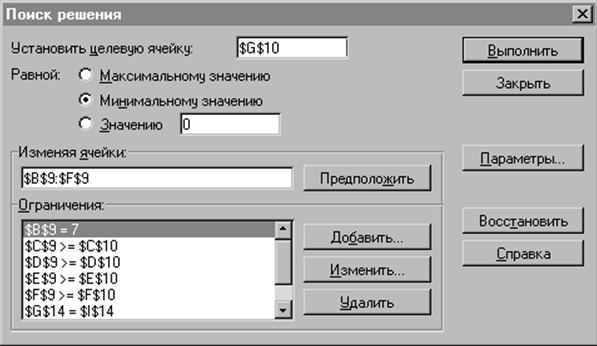
Рис. 26

Найденное решение

Рис. 27

Таким образом, дополнительные ресурсы равны: y₁=0, y₂=22, y₃=12. Это значит, что для заданного выпуска продукции необходимо иметь следующее количество ресурсов:

Ресурс1                    20+0=20

Ресурс2                    40+22=62                                                                            (14)

Ресурс3                    30+12=42

При этом будет получена прибыль, равная 390.