Принятие оптимальных решений. Методы решения задач линейного программирования, страница 4

1)   Ввести в ячейку F15=10. Решить задачу оптимизации для первого варианта с помощью команды Поиск решения.

2)   В окне Результаты поиска решения (рис. 12) нажать кнопку Сохранить сценарий.  На экране появится диалоговое окно Сохранить сценарий (рис. 18).

Рис. 18

3)   Ввести имя сценария: Ресурс2=10. Нажать кнопку ОК.

4)   Повторить действия, описанные в пунктах 1–3, для всех вариантов.

5)Для отображения отчета по результатам сценариев вызвать команду Сервис – Сценарии. На экране   появится диалоговое окно Диспетчер сценариев (рис. 19).

Рис. 19

6)  Нажать кнопку Отчет. Диалоговое окно Отчет по сценарию показано на рис. 20.

Рис. 20

7)   Выбрать переключатель Структура. Нажать кнопку ОК. На экране отображается отчет (рис. 21).

Рис. 21

Задача целочисленного программирования решаются аналогично задаче линейного программирования. При этом учитываются  требования целочисленности  переменных. Добавление соответствующих ограничений  осуществляется следующим образом:

1.      В диалоговом окне Поиск решения ( рис. 9) нажать кнопку Добавить. Появится диалоговое окно     Добавление ограничения. (рис. 22 ).

Рис. 22

2.   Указать, в какой ячейке находится целочисленная переменная. Открыть список Ограничение и выбрать в нем значение «целое».

Постановка задачи

Пример несовместных ограничений (8) и его графическая иллюстрация (рис. 6) приведены выше. Рассмотрим  решение задачи преодоления несовместности  с помощью  уже знакомой задачи распределения ресурсов.

Допустим, при решении задачи распределения ресурсов, кроме ранее рассмотренных ограничений,  надо учесть требование произвести 7 единиц изделий первого вида. Данной задаче соответствует следующая математическая модель:

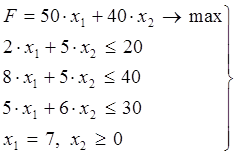                                                                       (11)

Очевидно, для выпуска указанного количества продукции ресурсов второго и третьего типа недостаточно. Если попытаться решить такую задачу с помощью Excel, то на экране появится окно с сообщением о невозможности найти подходящее решение (рис. 23). Это является признаком несовместности.

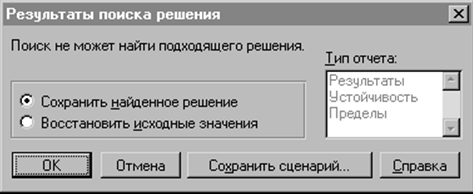
Рис. 23

Задача может быть решена лишь при увеличении имеющихся в нашем распоряжении ресурсов. Определим, каковы должны быть минимально необходимые дополнительные ресурсы для обеспечения выпуска требуемой продукции.

 Математическая модель

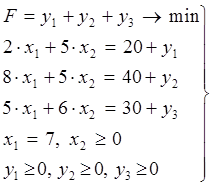  ,                                                              (12)

где :                y_i      –       минимально необходимый дополнительный ресурс i-го                                                          типа,                                                                                                    

Преобразуем модель к следующему виду:

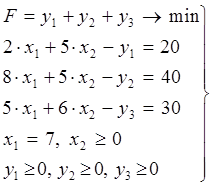                                                                 (13)